Question Number 33508 by EFG last updated on 18/Apr/18

$$\frac{\mathrm{3}^{{x}} ×\mathrm{8}^{{x}} }{\mathrm{12}^{{x}+\mathrm{1}} } \\ $$
Commented by Rasheed.Sindhi last updated on 18/Apr/18
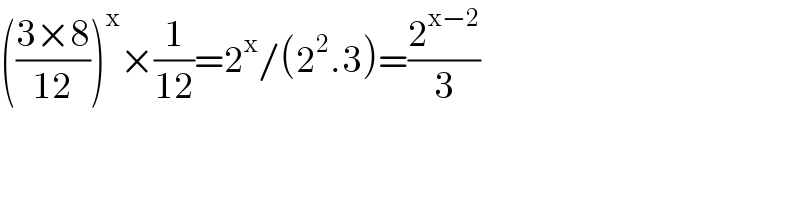
$$\left(\frac{\mathrm{3}×\mathrm{8}}{\mathrm{12}}\right)^{\mathrm{x}} ×\frac{\mathrm{1}}{\mathrm{12}}=\mathrm{2}^{\mathrm{x}} /\left(\mathrm{2}^{\mathrm{2}} .\mathrm{3}\right)=\frac{\mathrm{2}^{\mathrm{x}−\mathrm{2}} }{\mathrm{3}} \\ $$
Commented by math khazana by abdo last updated on 18/Apr/18
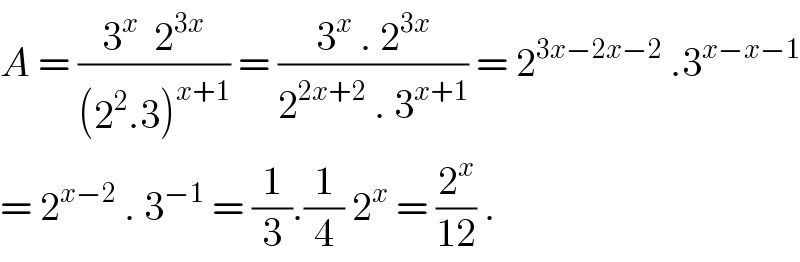
$${A}\:=\:\frac{\mathrm{3}^{{x}} \:\:\mathrm{2}^{\mathrm{3}{x}} }{\left(\mathrm{2}^{\mathrm{2}} .\mathrm{3}\right)^{{x}+\mathrm{1}} }\:=\:\frac{\mathrm{3}^{{x}} \:.\:\mathrm{2}^{\mathrm{3}{x}} }{\mathrm{2}^{\mathrm{2}{x}+\mathrm{2}} \:.\:\mathrm{3}^{{x}+\mathrm{1}} }\:=\:\mathrm{2}^{\mathrm{3}{x}−\mathrm{2}{x}−\mathrm{2}} \:.\mathrm{3}^{{x}−{x}−\mathrm{1}} \\ $$$$=\:\mathrm{2}^{{x}−\mathrm{2}} \:.\:\mathrm{3}^{−\mathrm{1}} \:=\:\frac{\mathrm{1}}{\mathrm{3}}.\frac{\mathrm{1}}{\mathrm{4}}\:\mathrm{2}^{{x}} \:=\:\frac{\mathrm{2}^{{x}} }{\mathrm{12}}\:. \\ $$
