Question Number 130678 by EDWIN88 last updated on 28/Jan/21
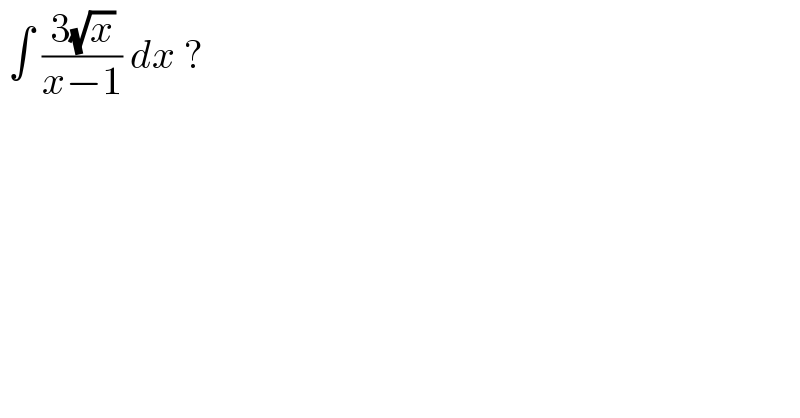
$$\:\int\:\frac{\mathrm{3}\sqrt{{x}}}{{x}−\mathrm{1}}\:{dx}\:?\: \\ $$
Answered by liberty last updated on 28/Jan/21
![L = ∫ ((3(√x))/(x−1)) dx ; [ x=u^2 ] L=6∫ (u^2 /(u^2 −1)) du = 6∫ (1+(1/(u^2 −1)))du L=6u+6∫ (du/(u^2 −1)) =6(√x) +3∫( (1/(u−1))−(1/(u+1)))du L=6(√x) +3ln ∣(((√x)−1)/( (√x)+1)) ∣ + c](https://www.tinkutara.com/question/Q130680.png)
$$\mathrm{L}\:=\:\int\:\frac{\mathrm{3}\sqrt{\mathrm{x}}}{\mathrm{x}−\mathrm{1}}\:\mathrm{dx}\:;\:\left[\:\mathrm{x}=\mathrm{u}^{\mathrm{2}} \:\right] \\ $$$$\mathrm{L}=\mathrm{6}\int\:\frac{\mathrm{u}^{\mathrm{2}} }{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}\:\mathrm{du}\:=\:\mathrm{6}\int\:\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}\right)\mathrm{du} \\ $$$$\mathrm{L}=\mathrm{6u}+\mathrm{6}\int\:\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}\:=\mathrm{6}\sqrt{\mathrm{x}}\:+\mathrm{3}\int\left(\:\frac{\mathrm{1}}{\mathrm{u}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{u}+\mathrm{1}}\right)\mathrm{du}\: \\ $$$$\mathrm{L}=\mathrm{6}\sqrt{\mathrm{x}}\:+\mathrm{3ln}\:\mid\frac{\sqrt{\mathrm{x}}−\mathrm{1}}{\:\sqrt{\mathrm{x}}+\mathrm{1}}\:\mid\:+\:\mathrm{c}\: \\ $$
