Question Number 79306 by jagoll last updated on 24/Jan/20

$$ \\ $$$$\sqrt{\mathrm{3}−\mathrm{x}}−\sqrt{\mathrm{x}+\mathrm{1}}>\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by kaivan.ahmadi last updated on 24/Jan/20
![3−x≥0⇒x≤3 x+1≥0⇒x≥−1 ⇒−1≤x≤3 3−x+x−1−2(√((3−x)(x+1)))>(1/4)⇒ −2(√((3−x)(x+1)))>−(7/4)⇒(√((3−x)(x+1)))<(7/8)⇒ (3−x)(x+1)<((49)/(64))⇒3−x^2 +2x+3<((49)/(64))⇒ x^2 −2x−((143)/(64))>0 Δ=4+((143)/(16))=((207)/(64)) x_(1,2) =((2±((√(207))/8))/2)=1±((√(207))/(16))=1±((3(√(23)))/(16)) x∈[−1,1−((3(√(23)))/(16))]∪[1+((3(√(23)))/(16)),3]](https://www.tinkutara.com/question/Q79324.png)
$$\mathrm{3}−{x}\geqslant\mathrm{0}\Rightarrow{x}\leqslant\mathrm{3} \\ $$$${x}+\mathrm{1}\geqslant\mathrm{0}\Rightarrow{x}\geqslant−\mathrm{1} \\ $$$$\Rightarrow−\mathrm{1}\leqslant{x}\leqslant\mathrm{3} \\ $$$$ \\ $$$$\mathrm{3}−{x}+{x}−\mathrm{1}−\mathrm{2}\sqrt{\left(\mathrm{3}−{x}\right)\left({x}+\mathrm{1}\right)}>\frac{\mathrm{1}}{\mathrm{4}}\Rightarrow \\ $$$$−\mathrm{2}\sqrt{\left(\mathrm{3}−{x}\right)\left({x}+\mathrm{1}\right)}>−\frac{\mathrm{7}}{\mathrm{4}}\Rightarrow\sqrt{\left(\mathrm{3}−{x}\right)\left({x}+\mathrm{1}\right)}<\frac{\mathrm{7}}{\mathrm{8}}\Rightarrow \\ $$$$\left(\mathrm{3}−{x}\right)\left({x}+\mathrm{1}\right)<\frac{\mathrm{49}}{\mathrm{64}}\Rightarrow\mathrm{3}−{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{3}<\frac{\mathrm{49}}{\mathrm{64}}\Rightarrow \\ $$$${x}^{\mathrm{2}} −\mathrm{2}{x}−\frac{\mathrm{143}}{\mathrm{64}}>\mathrm{0} \\ $$$$\Delta=\mathrm{4}+\frac{\mathrm{143}}{\mathrm{16}}=\frac{\mathrm{207}}{\mathrm{64}} \\ $$$${x}_{\mathrm{1},\mathrm{2}} =\frac{\mathrm{2}\pm\frac{\sqrt{\mathrm{207}}}{\mathrm{8}}}{\mathrm{2}}=\mathrm{1}\pm\frac{\sqrt{\mathrm{207}}}{\mathrm{16}}=\mathrm{1}\pm\frac{\mathrm{3}\sqrt{\mathrm{23}}}{\mathrm{16}} \\ $$$${x}\in\left[−\mathrm{1},\mathrm{1}−\frac{\mathrm{3}\sqrt{\mathrm{23}}}{\mathrm{16}}\right]\cup\left[\mathrm{1}+\frac{\mathrm{3}\sqrt{\mathrm{23}}}{\mathrm{16}},\mathrm{3}\right] \\ $$$$ \\ $$
Commented by key of knowledge last updated on 24/Jan/20

$$\mathrm{ahmadi}\:\mathrm{aziz},\mathrm{for}\:\mathrm{x}=\mathrm{3}: \\ $$$$\sqrt{\mathrm{3}−\mathrm{3}}−\sqrt{\mathrm{3}+\mathrm{1}}=\mathrm{0}−\mathrm{2}=−\mathrm{2}\ngtr\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$
Commented by kaivan.ahmadi last updated on 24/Jan/20

$${Hi}\:{sir},\:{thank}\:{you}. \\ $$$${I}\:{did}\:{err}\:,\:{in}\:{line}\:\mathrm{4} \\ $$$$\mathrm{3}−{x}+{x}+\mathrm{1} \\ $$
Commented by kaivan.ahmadi last updated on 24/Jan/20

$${aziz}\:{delam} \\ $$
Commented by john santu last updated on 24/Jan/20
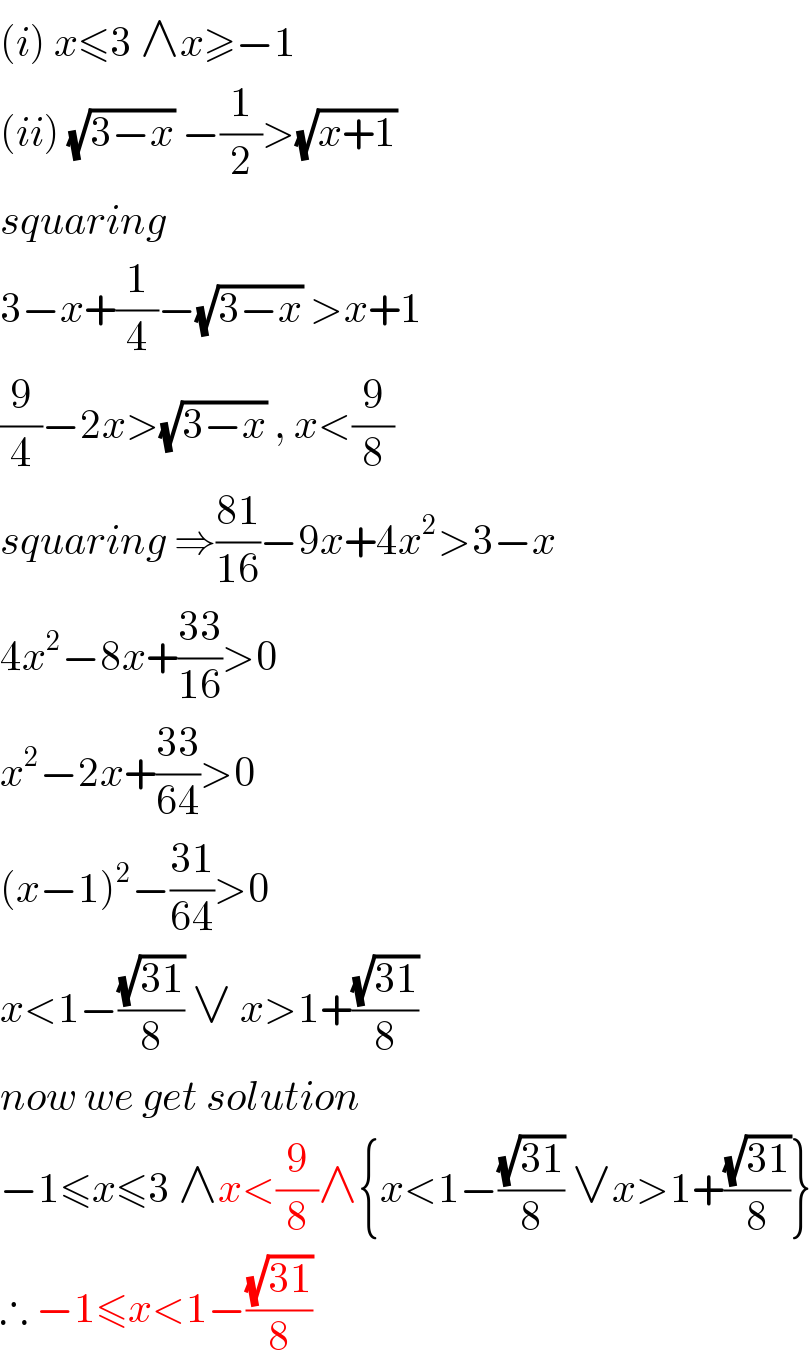
$$\left({i}\right)\:{x}\leqslant\mathrm{3}\:\wedge{x}\geqslant−\mathrm{1} \\ $$$$\left({ii}\right)\:\sqrt{\mathrm{3}−{x}}\:−\frac{\mathrm{1}}{\mathrm{2}}>\sqrt{{x}+\mathrm{1}} \\ $$$${squaring}\: \\ $$$$\mathrm{3}−{x}+\frac{\mathrm{1}}{\mathrm{4}}−\sqrt{\mathrm{3}−{x}}\:>{x}+\mathrm{1} \\ $$$$\frac{\mathrm{9}}{\mathrm{4}}−\mathrm{2}{x}>\sqrt{\mathrm{3}−{x}}\:,\:{x}<\frac{\mathrm{9}}{\mathrm{8}} \\ $$$${squaring}\:\Rightarrow\frac{\mathrm{81}}{\mathrm{16}}−\mathrm{9}{x}+\mathrm{4}{x}^{\mathrm{2}} >\mathrm{3}−{x} \\ $$$$\mathrm{4}{x}^{\mathrm{2}} −\mathrm{8}{x}+\frac{\mathrm{33}}{\mathrm{16}}>\mathrm{0} \\ $$$${x}^{\mathrm{2}} −\mathrm{2}{x}+\frac{\mathrm{33}}{\mathrm{64}}>\mathrm{0} \\ $$$$\left({x}−\mathrm{1}\right)^{\mathrm{2}} −\frac{\mathrm{31}}{\mathrm{64}}>\mathrm{0} \\ $$$${x}<\mathrm{1}−\frac{\sqrt{\mathrm{31}}}{\mathrm{8}}\:\vee\:{x}>\mathrm{1}+\frac{\sqrt{\mathrm{31}}}{\mathrm{8}} \\ $$$${now}\:{we}\:{get}\:{solution} \\ $$$$−\mathrm{1}\leqslant{x}\leqslant\mathrm{3}\:\wedge{x}<\frac{\mathrm{9}}{\mathrm{8}}\wedge\left\{{x}<\mathrm{1}−\frac{\sqrt{\mathrm{31}}}{\mathrm{8}}\:\vee{x}>\mathrm{1}+\frac{\sqrt{\mathrm{31}}}{\mathrm{8}}\right\} \\ $$$$\therefore\:−\mathrm{1}\leqslant{x}<\mathrm{1}−\frac{\sqrt{\mathrm{31}}}{\mathrm{8}}\:\: \\ $$
Commented by john santu last updated on 24/Jan/20

$${by}\:{cheking}\: \\ $$$${x}\:\in\left[−\mathrm{1},\mathrm{1}−\frac{\sqrt{\mathrm{31}}}{\mathrm{8}}\right)\:\Rightarrow\:\left[−\mathrm{1},\:\mathrm{0}.\mathrm{304}\right) \\ $$$${put}\:{x}\:=\:\mathrm{0}.\mathrm{2}\:\Rightarrow\sqrt{\mathrm{3}−\mathrm{0}.\mathrm{2}}−\sqrt{\mathrm{1}+\mathrm{0}.\mathrm{2}} \\ $$$$=\mathrm{1}.\mathrm{673}−\mathrm{1}.\mathrm{095}\:=\mathrm{0}.\mathrm{578}\:.\:{true} \\ $$
Commented by jagoll last updated on 24/Jan/20

$$\mathrm{thank}\:\mathrm{you} \\ $$
Answered by key of knowledge last updated on 24/Jan/20
![3−x≥0∧x+1≥0⇒−1≤x≤3 (i) (√(3−x))>(√(x+1))+(1/2)⇒3−x>(1/4)+x+1+(√(x+1))⇒ (7/4)−2x>(√(x+1)) ((√(x+1))≥0⇒(7/4)−2x≥0⇒x≤(7/8) (ii)) 4x^2 −8x+((33)/(16))>0⇒((8+(√(31)))/8)<x∨x<((8−(√(31)))/8) (iii) i∩ii∩iii=[−1,((8−(√(31)))/8)]](https://www.tinkutara.com/question/Q79339.png)
$$\mathrm{3}−\mathrm{x}\geqslant\mathrm{0}\wedge\mathrm{x}+\mathrm{1}\geqslant\mathrm{0}\Rightarrow−\mathrm{1}\leqslant\mathrm{x}\leqslant\mathrm{3}\:\left(\mathrm{i}\right) \\ $$$$\sqrt{\mathrm{3}−\mathrm{x}}>\sqrt{\mathrm{x}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\mathrm{3}−\mathrm{x}>\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{x}+\mathrm{1}+\sqrt{\mathrm{x}+\mathrm{1}}\Rightarrow \\ $$$$\frac{\mathrm{7}}{\mathrm{4}}−\mathrm{2x}>\sqrt{\mathrm{x}+\mathrm{1}}\:\:\:\left(\sqrt{\mathrm{x}+\mathrm{1}}\geqslant\mathrm{0}\Rightarrow\frac{\mathrm{7}}{\mathrm{4}}−\mathrm{2x}\geqslant\mathrm{0}\Rightarrow\mathrm{x}\leqslant\frac{\mathrm{7}}{\mathrm{8}}\:\left(\mathrm{ii}\right)\right) \\ $$$$\mathrm{4x}^{\mathrm{2}} −\mathrm{8x}+\frac{\mathrm{33}}{\mathrm{16}}>\mathrm{0}\Rightarrow\frac{\mathrm{8}+\sqrt{\mathrm{31}}}{\mathrm{8}}<\mathrm{x}\vee\mathrm{x}<\frac{\mathrm{8}−\sqrt{\mathrm{31}}}{\mathrm{8}}\:\:\left(\mathrm{iii}\right) \\ $$$$\mathrm{i}\cap\mathrm{ii}\cap\mathrm{iii}=\left[−\mathrm{1},\frac{\mathrm{8}−\sqrt{\mathrm{31}}}{\mathrm{8}}\right] \\ $$
