Question Number 24938 by kosarrr last updated on 29/Nov/17
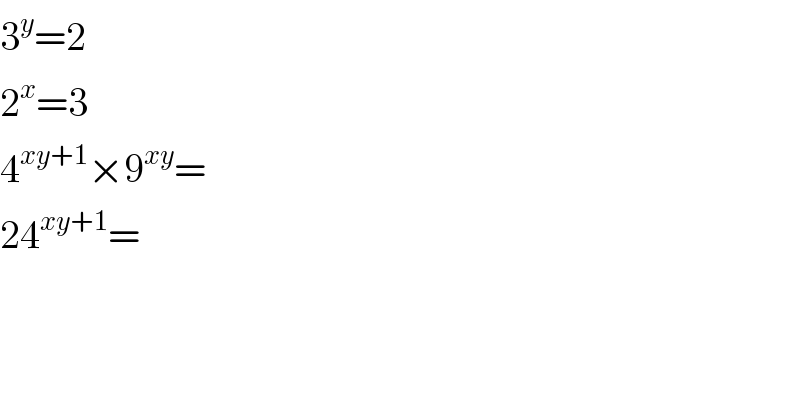
$$\mathrm{3}^{{y}} =\mathrm{2} \\ $$$$\mathrm{2}^{{x}} =\mathrm{3} \\ $$$$\mathrm{4}^{{xy}+\mathrm{1}} ×\mathrm{9}^{{xy}} = \\ $$$$\mathrm{24}^{{xy}+\mathrm{1}} = \\ $$
Commented by prakash jain last updated on 29/Nov/17
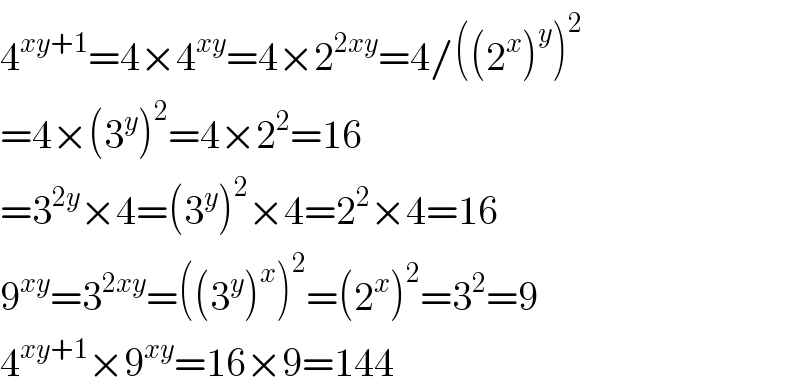
$$\mathrm{4}^{{xy}+\mathrm{1}} =\mathrm{4}×\mathrm{4}^{{xy}} =\mathrm{4}×\mathrm{2}^{\mathrm{2}{xy}} =\mathrm{4}/\left(\left(\mathrm{2}^{{x}} \right)^{{y}} \right)^{\mathrm{2}} \\ $$$$=\mathrm{4}×\left(\mathrm{3}^{{y}} \right)^{\mathrm{2}} =\mathrm{4}×\mathrm{2}^{\mathrm{2}} =\mathrm{16} \\ $$$$=\mathrm{3}^{\mathrm{2}{y}} ×\mathrm{4}=\left(\mathrm{3}^{{y}} \right)^{\mathrm{2}} ×\mathrm{4}=\mathrm{2}^{\mathrm{2}} ×\mathrm{4}=\mathrm{16} \\ $$$$\mathrm{9}^{{xy}} =\mathrm{3}^{\mathrm{2}{xy}} =\left(\left(\mathrm{3}^{{y}} \right)^{{x}} \right)^{\mathrm{2}} =\left(\mathrm{2}^{{x}} \right)^{\mathrm{2}} =\mathrm{3}^{\mathrm{2}} =\mathrm{9} \\ $$$$\mathrm{4}^{{xy}+\mathrm{1}} ×\mathrm{9}^{{xy}} =\mathrm{16}×\mathrm{9}=\mathrm{144} \\ $$
