Question Number 63602 by pavithra last updated on 06/Jul/19
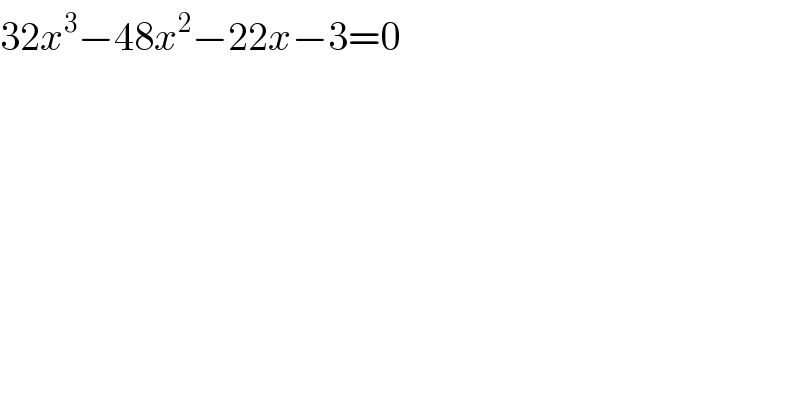
$$\mathrm{32}{x}^{\mathrm{3}} −\mathrm{48}{x}^{\mathrm{2}} −\mathrm{22}{x}−\mathrm{3}=\mathrm{0} \\ $$
Answered by MJS last updated on 06/Jul/19
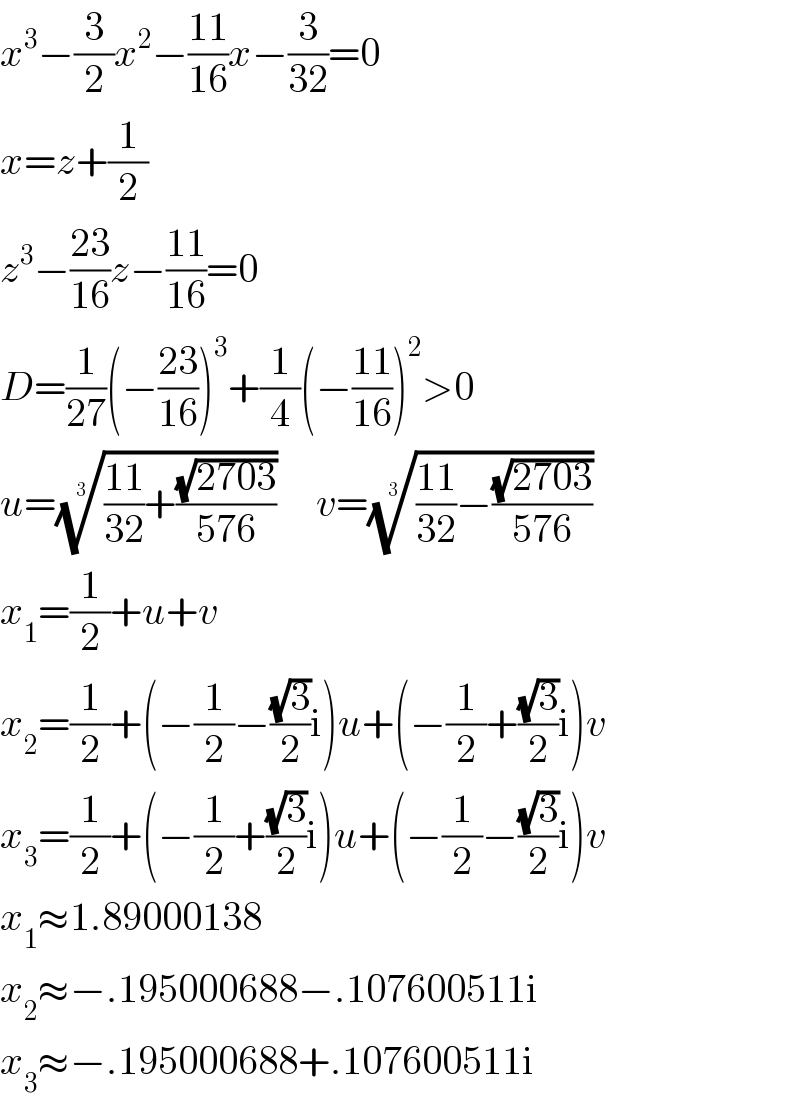
$${x}^{\mathrm{3}} −\frac{\mathrm{3}}{\mathrm{2}}{x}^{\mathrm{2}} −\frac{\mathrm{11}}{\mathrm{16}}{x}−\frac{\mathrm{3}}{\mathrm{32}}=\mathrm{0} \\ $$$${x}={z}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${z}^{\mathrm{3}} −\frac{\mathrm{23}}{\mathrm{16}}{z}−\frac{\mathrm{11}}{\mathrm{16}}=\mathrm{0} \\ $$$${D}=\frac{\mathrm{1}}{\mathrm{27}}\left(−\frac{\mathrm{23}}{\mathrm{16}}\right)^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{4}}\left(−\frac{\mathrm{11}}{\mathrm{16}}\right)^{\mathrm{2}} >\mathrm{0} \\ $$$${u}=\sqrt[{\mathrm{3}}]{\frac{\mathrm{11}}{\mathrm{32}}+\frac{\sqrt{\mathrm{2703}}}{\mathrm{576}}}\:\:\:\:\:{v}=\sqrt[{\mathrm{3}}]{\frac{\mathrm{11}}{\mathrm{32}}−\frac{\sqrt{\mathrm{2703}}}{\mathrm{576}}} \\ $$$${x}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}+{u}+{v} \\ $$$${x}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}+\left(−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right){u}+\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right){v} \\ $$$${x}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{2}}+\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right){u}+\left(−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right){v} \\ $$$${x}_{\mathrm{1}} \approx\mathrm{1}.\mathrm{89000138} \\ $$$${x}_{\mathrm{2}} \approx−.\mathrm{195000688}−.\mathrm{107600511i} \\ $$$${x}_{\mathrm{3}} \approx−.\mathrm{195000688}+.\mathrm{107600511i} \\ $$
Commented by pavithra last updated on 07/Jul/19

$${thankyou} \\ $$
Answered by ajfour last updated on 07/Jul/19
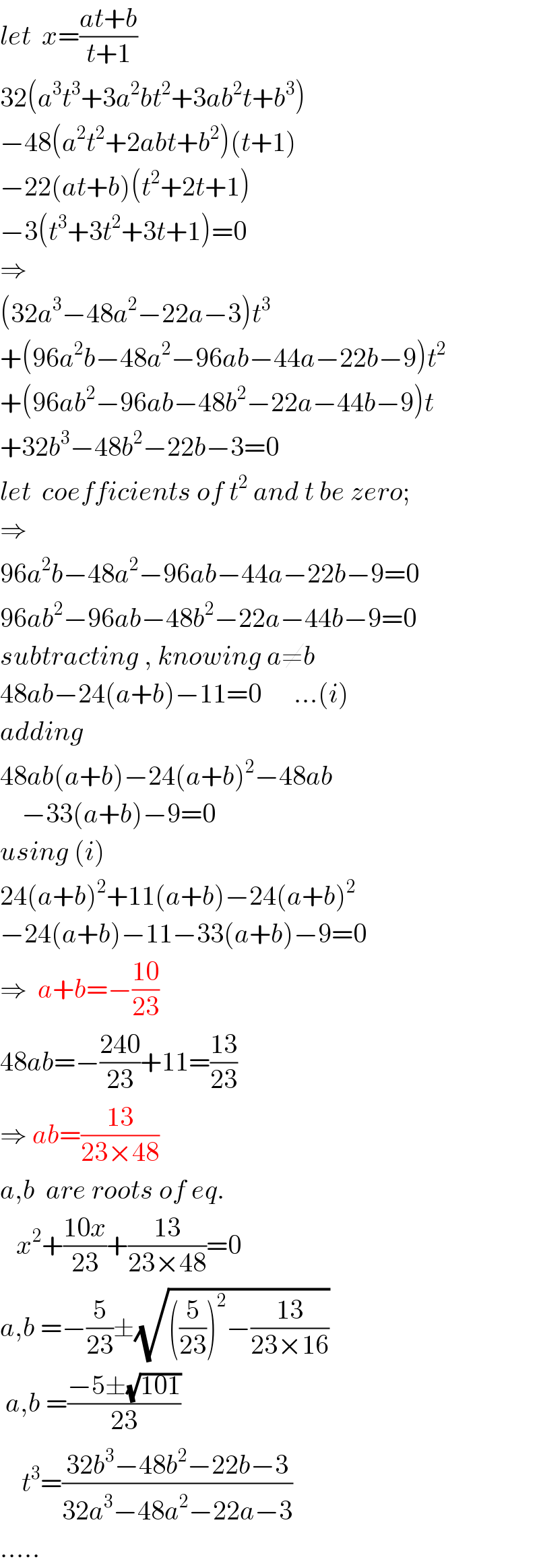
$${let}\:\:{x}=\frac{{at}+{b}}{{t}+\mathrm{1}} \\ $$$$\mathrm{32}\left({a}^{\mathrm{3}} {t}^{\mathrm{3}} +\mathrm{3}{a}^{\mathrm{2}} {bt}^{\mathrm{2}} +\mathrm{3}{ab}^{\mathrm{2}} {t}+{b}^{\mathrm{3}} \right) \\ $$$$−\mathrm{48}\left({a}^{\mathrm{2}} {t}^{\mathrm{2}} +\mathrm{2}{abt}+{b}^{\mathrm{2}} \right)\left({t}+\mathrm{1}\right) \\ $$$$−\mathrm{22}\left({at}+{b}\right)\left({t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}\right) \\ $$$$−\mathrm{3}\left({t}^{\mathrm{3}} +\mathrm{3}{t}^{\mathrm{2}} +\mathrm{3}{t}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\left(\mathrm{32}{a}^{\mathrm{3}} −\mathrm{48}{a}^{\mathrm{2}} −\mathrm{22}{a}−\mathrm{3}\right){t}^{\mathrm{3}} \\ $$$$+\left(\mathrm{96}{a}^{\mathrm{2}} {b}−\mathrm{48}{a}^{\mathrm{2}} −\mathrm{96}{ab}−\mathrm{44}{a}−\mathrm{22}{b}−\mathrm{9}\right){t}^{\mathrm{2}} \\ $$$$+\left(\mathrm{96}{ab}^{\mathrm{2}} −\mathrm{96}{ab}−\mathrm{48}{b}^{\mathrm{2}} −\mathrm{22}{a}−\mathrm{44}{b}−\mathrm{9}\right){t} \\ $$$$+\mathrm{32}{b}^{\mathrm{3}} −\mathrm{48}{b}^{\mathrm{2}} −\mathrm{22}{b}−\mathrm{3}=\mathrm{0} \\ $$$${let}\:\:{coefficients}\:{of}\:{t}^{\mathrm{2}} \:{and}\:{t}\:{be}\:{zero}; \\ $$$$\Rightarrow \\ $$$$\mathrm{96}{a}^{\mathrm{2}} {b}−\mathrm{48}{a}^{\mathrm{2}} −\mathrm{96}{ab}−\mathrm{44}{a}−\mathrm{22}{b}−\mathrm{9}=\mathrm{0} \\ $$$$\mathrm{96}{ab}^{\mathrm{2}} −\mathrm{96}{ab}−\mathrm{48}{b}^{\mathrm{2}} −\mathrm{22}{a}−\mathrm{44}{b}−\mathrm{9}=\mathrm{0} \\ $$$${subtracting}\:,\:{knowing}\:{a}\neq{b} \\ $$$$\mathrm{48}{ab}−\mathrm{24}\left({a}+{b}\right)−\mathrm{11}=\mathrm{0}\:\:\:\:\:\:…\left({i}\right) \\ $$$${adding} \\ $$$$\mathrm{48}{ab}\left({a}+{b}\right)−\mathrm{24}\left({a}+{b}\right)^{\mathrm{2}} −\mathrm{48}{ab} \\ $$$$\:\:\:\:−\mathrm{33}\left({a}+{b}\right)−\mathrm{9}=\mathrm{0} \\ $$$${using}\:\left({i}\right) \\ $$$$\mathrm{24}\left({a}+{b}\right)^{\mathrm{2}} +\mathrm{11}\left({a}+{b}\right)−\mathrm{24}\left({a}+{b}\right)^{\mathrm{2}} \\ $$$$−\mathrm{24}\left({a}+{b}\right)−\mathrm{11}−\mathrm{33}\left({a}+{b}\right)−\mathrm{9}=\mathrm{0} \\ $$$$\Rightarrow\:\:{a}+{b}=−\frac{\mathrm{10}}{\mathrm{23}} \\ $$$$\mathrm{48}{ab}=−\frac{\mathrm{240}}{\mathrm{23}}+\mathrm{11}=\frac{\mathrm{13}}{\mathrm{23}} \\ $$$$\Rightarrow\:{ab}=\frac{\mathrm{13}}{\mathrm{23}×\mathrm{48}} \\ $$$${a},{b}\:\:{are}\:{roots}\:{of}\:{eq}. \\ $$$$\:\:\:{x}^{\mathrm{2}} +\frac{\mathrm{10}{x}}{\mathrm{23}}+\frac{\mathrm{13}}{\mathrm{23}×\mathrm{48}}=\mathrm{0} \\ $$$${a},{b}\:=−\frac{\mathrm{5}}{\mathrm{23}}\pm\sqrt{\left(\frac{\mathrm{5}}{\mathrm{23}}\right)^{\mathrm{2}} −\frac{\mathrm{13}}{\mathrm{23}×\mathrm{16}}} \\ $$$$\:{a},{b}\:=\frac{−\mathrm{5}\pm\sqrt{\mathrm{101}}}{\mathrm{23}} \\ $$$$\:\:\:\:{t}^{\mathrm{3}} =\frac{\mathrm{32}{b}^{\mathrm{3}} −\mathrm{48}{b}^{\mathrm{2}} −\mathrm{22}{b}−\mathrm{3}}{\mathrm{32}{a}^{\mathrm{3}} −\mathrm{48}{a}^{\mathrm{2}} −\mathrm{22}{a}−\mathrm{3}} \\ $$$$….. \\ $$
