Question Number 156319 by cortano last updated on 10/Oct/21
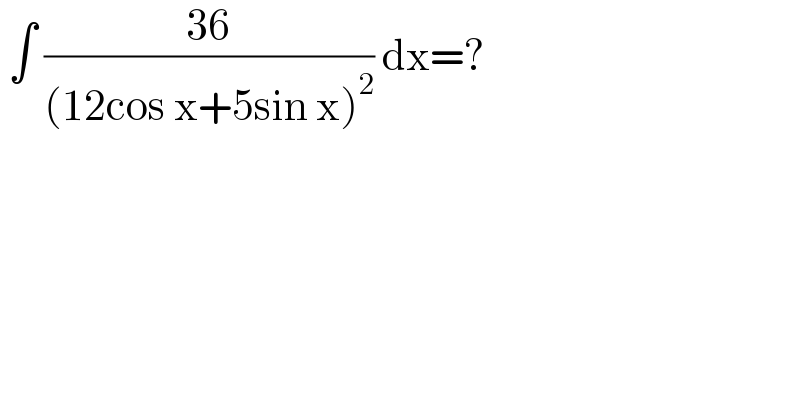
$$\:\int\:\frac{\mathrm{36}}{\left(\mathrm{12cos}\:\mathrm{x}+\mathrm{5sin}\:\mathrm{x}\right)^{\mathrm{2}} }\:\mathrm{dx}=? \\ $$
Commented by john_santu last updated on 10/Oct/21

$$=\frac{\mathrm{36}}{\mathrm{13}}\left(\frac{\mathrm{12sin}\:{x}−\mathrm{5cos}\:{x}}{\mathrm{5sin}\:{x}+\mathrm{12cos}\:{x}}\right)+{c} \\ $$
Answered by puissant last updated on 10/Oct/21

$$=\int\frac{\mathrm{36}}{{cos}^{\mathrm{2}} {x}\left(\mathrm{12}+\mathrm{5}{tan}^{\mathrm{2}} {x}\right)}{dx}\overset{{u}={tanx}} {=}\int\frac{\mathrm{36}}{\mathrm{12}+\mathrm{5}{u}^{\mathrm{2}} }{du} \\ $$$$=\mathrm{3}\int\frac{{du}}{\mathrm{1}+\left(\sqrt{\frac{\mathrm{5}}{\mathrm{12}}}{u}\right)^{\mathrm{2}} }\overset{{t}=\sqrt{\frac{\mathrm{5}}{\mathrm{12}}}{u}} {=}\frac{\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{2}\sqrt{\mathrm{3}}}\int\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\:\frac{\sqrt{\mathrm{15}}}{\mathrm{2}}\:{arctan}\left({t}\right)+{C} \\ $$$$ \\ $$$$\:\:\therefore\because\:{K}=\:\int\frac{\mathrm{36}}{\left(\mathrm{12}{cosx}+\mathrm{5}{sinx}\right)^{\mathrm{2}} }{dx}=\frac{\sqrt{\mathrm{15}}}{\mathrm{2}}\:{arctan}\left(\sqrt{\frac{\mathrm{5}}{\mathrm{12}}}{tanx}\right)+{C} \\ $$
