Question Number 37155 by ajfour last updated on 09/Jun/18
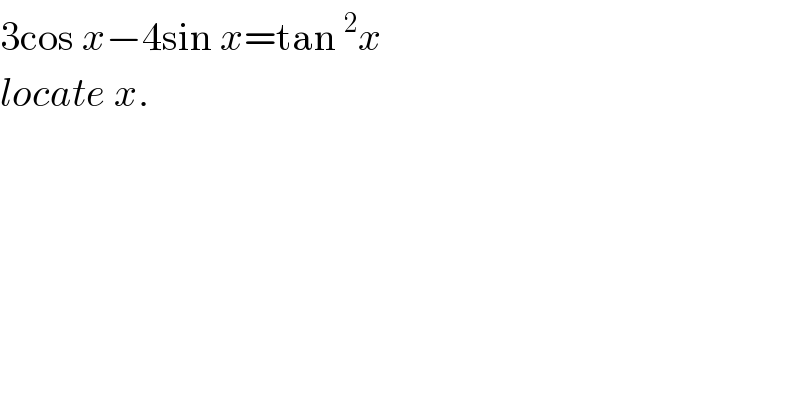
$$\mathrm{3cos}\:{x}−\mathrm{4sin}\:{x}=\mathrm{tan}\:^{\mathrm{2}} {x} \\ $$$${locate}\:{x}. \\ $$
Commented by behi83417@gmail.com last updated on 09/Jun/18
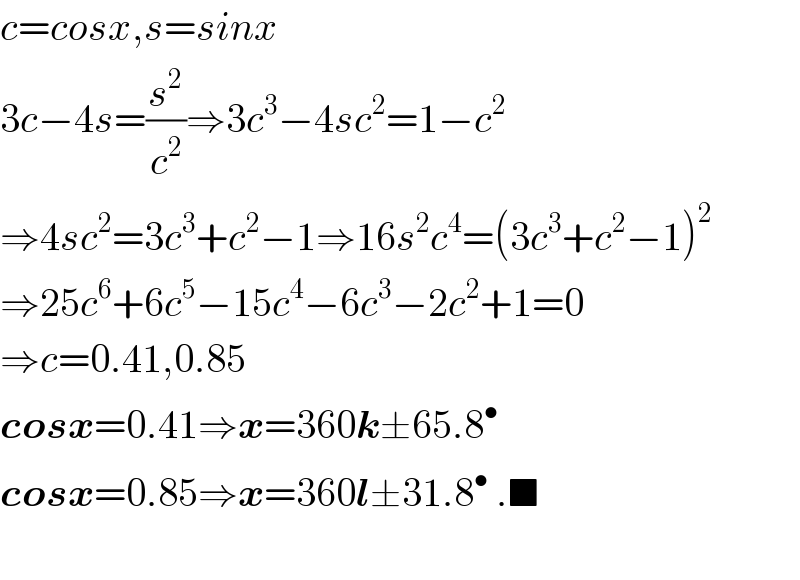
$${c}={cosx},{s}={sinx} \\ $$$$\mathrm{3}{c}−\mathrm{4}{s}=\frac{{s}^{\mathrm{2}} }{{c}^{\mathrm{2}} }\Rightarrow\mathrm{3}{c}^{\mathrm{3}} −\mathrm{4}{sc}^{\mathrm{2}} =\mathrm{1}−{c}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{4}{sc}^{\mathrm{2}} =\mathrm{3}{c}^{\mathrm{3}} +{c}^{\mathrm{2}} −\mathrm{1}\Rightarrow\mathrm{16}{s}^{\mathrm{2}} {c}^{\mathrm{4}} =\left(\mathrm{3}{c}^{\mathrm{3}} +{c}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{25}{c}^{\mathrm{6}} +\mathrm{6}{c}^{\mathrm{5}} −\mathrm{15}{c}^{\mathrm{4}} −\mathrm{6}{c}^{\mathrm{3}} −\mathrm{2}{c}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{c}=\mathrm{0}.\mathrm{41},\mathrm{0}.\mathrm{85} \\ $$$$\boldsymbol{{cosx}}=\mathrm{0}.\mathrm{41}\Rightarrow\boldsymbol{{x}}=\mathrm{360}\boldsymbol{{k}}\pm\mathrm{65}.\mathrm{8}^{\bullet} \\ $$$$\boldsymbol{{cosx}}=\mathrm{0}.\mathrm{85}\Rightarrow\boldsymbol{{x}}=\mathrm{360}\boldsymbol{{l}}\pm\mathrm{31}.\mathrm{8}^{\bullet} \:.\blacksquare \\ $$$$ \\ $$
Commented by ajfour last updated on 10/Jun/18
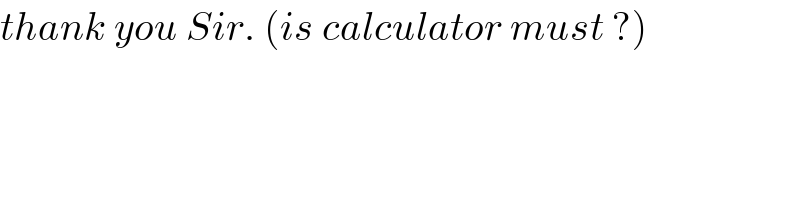
$${thank}\:{you}\:{Sir}.\:\left({is}\:{calculator}\:{must}\:?\right) \\ $$
Commented by MJS last updated on 10/Jun/18
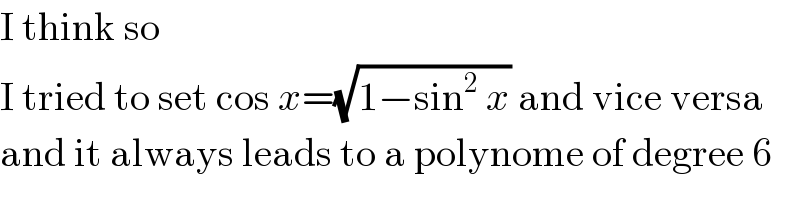
$$\mathrm{I}\:\mathrm{think}\:\mathrm{so} \\ $$$$\mathrm{I}\:\mathrm{tried}\:\mathrm{to}\:\mathrm{set}\:\mathrm{cos}\:{x}=\sqrt{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:{x}}\:\mathrm{and}\:\mathrm{vice}\:\mathrm{versa} \\ $$$$\mathrm{and}\:\mathrm{it}\:\mathrm{always}\:\mathrm{leads}\:\mathrm{to}\:\mathrm{a}\:\mathrm{polynome}\:\mathrm{of}\:\mathrm{degree}\:\mathrm{6} \\ $$
Commented by ajfour last updated on 10/Jun/18
$${Sir}\:{please}\:{attempt}\:{Q}.\mathrm{37166}\:{also}. \\ $$
