Question Number 183381 by Shrinava last updated on 25/Dec/22
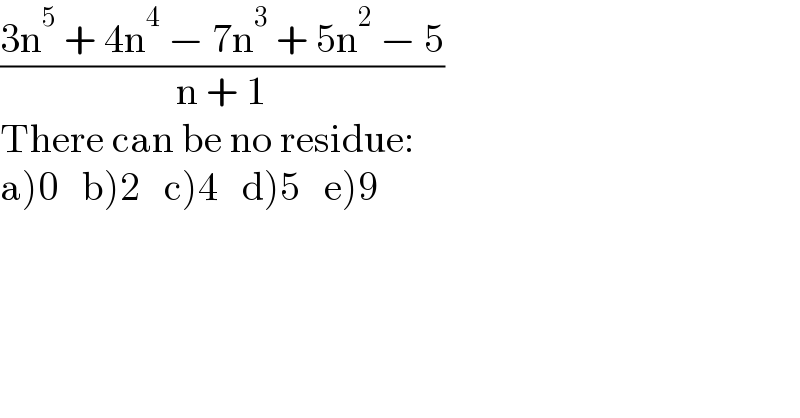
$$\frac{\mathrm{3n}^{\mathrm{5}} \:+\:\mathrm{4n}^{\mathrm{4}} \:−\:\mathrm{7n}^{\mathrm{3}} \:+\:\mathrm{5n}^{\mathrm{2}} \:−\:\mathrm{5}}{\mathrm{n}\:+\:\mathrm{1}} \\ $$$$\mathrm{There}\:\mathrm{can}\:\mathrm{be}\:\mathrm{no}\:\mathrm{residue}: \\ $$$$\left.\mathrm{a}\left.\right)\left.\mathrm{0}\left.\:\left.\:\:\mathrm{b}\right)\mathrm{2}\:\:\:\mathrm{c}\right)\mathrm{4}\:\:\:\mathrm{d}\right)\mathrm{5}\:\:\:\mathrm{e}\right)\mathrm{9} \\ $$
Commented by Shrinava last updated on 25/Dec/22

$$\mathrm{sorry}:\:\:\mathrm{5n}^{\mathrm{2}} \:−\:\mathrm{4} \\ $$
Commented by Frix last updated on 25/Dec/22

$$\mathrm{same}\:\mathrm{answer} \\ $$
Answered by Frix last updated on 25/Dec/22
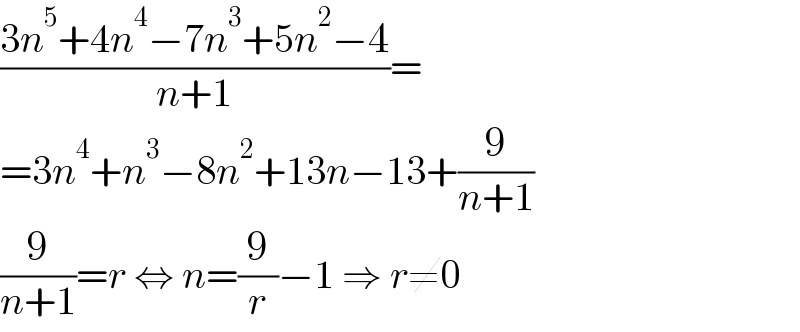
$$\frac{\mathrm{3}{n}^{\mathrm{5}} +\mathrm{4}{n}^{\mathrm{4}} −\mathrm{7}{n}^{\mathrm{3}} +\mathrm{5}{n}^{\mathrm{2}} −\mathrm{4}}{{n}+\mathrm{1}}= \\ $$$$=\mathrm{3}{n}^{\mathrm{4}} +{n}^{\mathrm{3}} −\mathrm{8}{n}^{\mathrm{2}} +\mathrm{13}{n}−\mathrm{13}+\frac{\mathrm{9}}{{n}+\mathrm{1}} \\ $$$$\frac{\mathrm{9}}{{n}+\mathrm{1}}={r}\:\Leftrightarrow\:{n}=\frac{\mathrm{9}}{{r}}−\mathrm{1}\:\Rightarrow\:{r}\neq\mathrm{0} \\ $$
