Question Number 157230 by Jamshidbek last updated on 21/Oct/21

$$\left(\mathrm{3x}+\mathrm{1}\right)^{\mathrm{100}} \:\: \\ $$$$\mathrm{Find}\:\mathrm{this}\:\mathrm{max}\:\mathrm{Koeffitcient} \\ $$
Answered by mr W last updated on 21/Oct/21
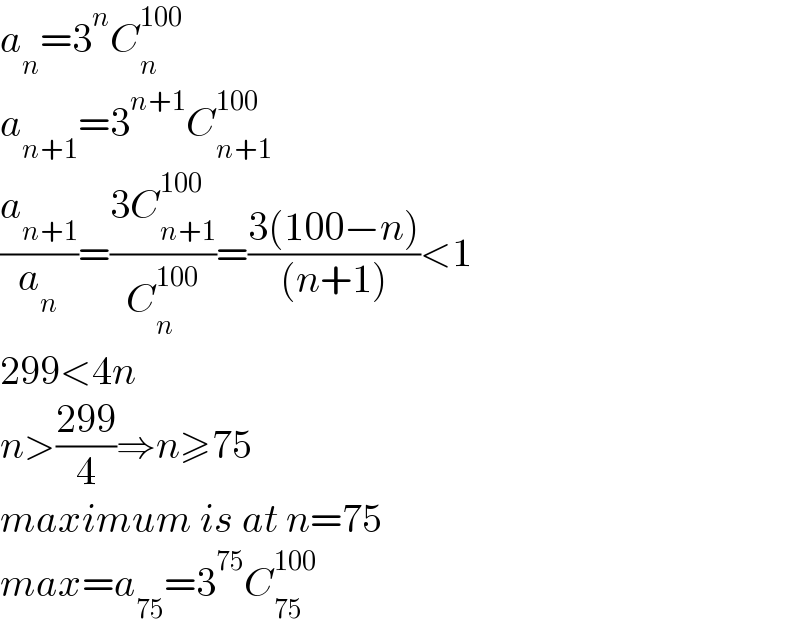
$${a}_{{n}} =\mathrm{3}^{{n}} {C}_{{n}} ^{\mathrm{100}} \\ $$$${a}_{{n}+\mathrm{1}} =\mathrm{3}^{{n}+\mathrm{1}} {C}_{{n}+\mathrm{1}} ^{\mathrm{100}} \\ $$$$\frac{{a}_{{n}+\mathrm{1}} }{{a}_{{n}} }=\frac{\mathrm{3}{C}_{{n}+\mathrm{1}} ^{\mathrm{100}} }{{C}_{{n}} ^{\mathrm{100}} }=\frac{\mathrm{3}\left(\mathrm{100}−{n}\right)}{\left({n}+\mathrm{1}\right)}<\mathrm{1} \\ $$$$\mathrm{299}<\mathrm{4}{n} \\ $$$${n}>\frac{\mathrm{299}}{\mathrm{4}}\Rightarrow{n}\geqslant\mathrm{75} \\ $$$${maximum}\:{is}\:{at}\:{n}=\mathrm{75} \\ $$$${max}={a}_{\mathrm{75}} =\mathrm{3}^{\mathrm{75}} {C}_{\mathrm{75}} ^{\mathrm{100}} \\ $$
Commented by Tawa11 last updated on 21/Oct/21

$$\mathrm{Great}\:\mathrm{sir} \\ $$
