3x-1-4x-x-2-dx-

Question Number 169054 by MikeH last updated on 23/Apr/22

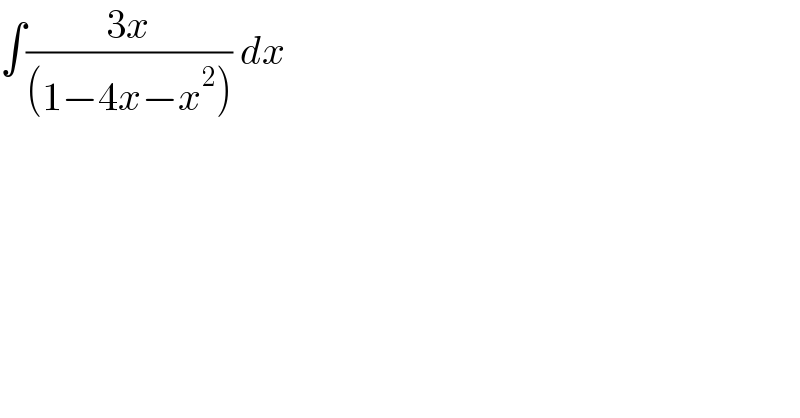
$$\int\frac{\mathrm{3}{x}}{\left(\mathrm{1}−\mathrm{4}{x}−{x}^{\mathrm{2}} \right)}\:{dx} \\ $$

Answered by haladu last updated on 23/Apr/22

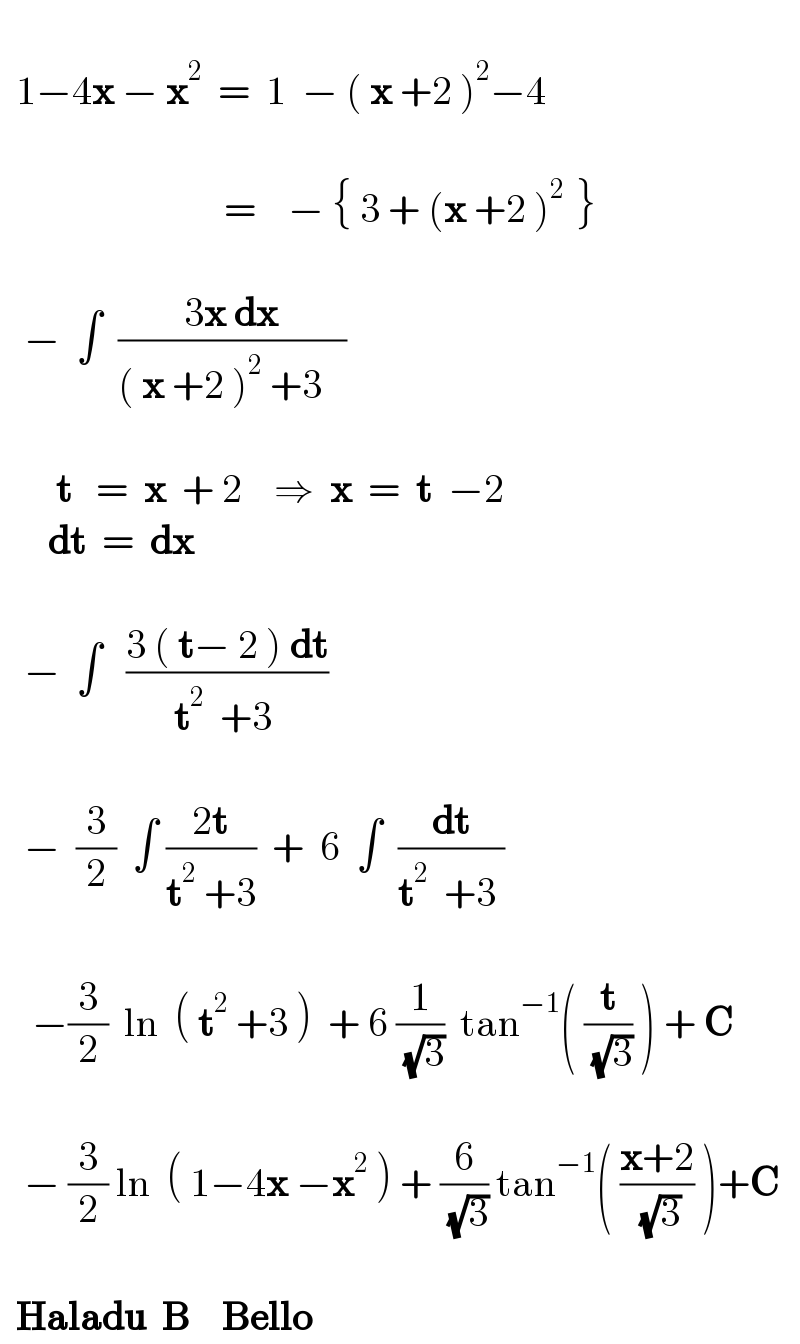
1−4x − x^2 = 1 − ( x +2 )^2 −4 = − { 3 + (x +2 )^(2 ) } − ∫ ((3x dx)/(( x +2 )^2 +3 )) t = x + 2 ⇒ x = t −2 dt = dx − ∫ ((3 ( t− 2 ) dt)/(t^2 +3 )) − (3/2) ∫ ((2t)/(t^2 +3)) + 6 ∫ (dt/(t^2 +3 )) −(3/2) ln ( t^2 +3 ) + 6 (1/( (√3))) tan^(−1) ( (t/( (√3))) ) + C − (3/2) ln ( 1−4x −x^2 ) + (6/( (√3))) tan^(−1) ( ((x+2)/( (√3))) )+C Haladu B Bello

$$\:\: \\ $$$$\:\:\mathrm{1}−\mathrm{4}\boldsymbol{\mathrm{x}}\:−\:\boldsymbol{\mathrm{x}}^{\mathrm{2}} \:\:=\:\:\mathrm{1}\:\:−\:\left(\:\boldsymbol{\mathrm{x}}\:+\mathrm{2}\:\right)^{\mathrm{2}} −\mathrm{4}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\:\:−\:\left\{\:\mathrm{3}\:+\:\left(\boldsymbol{\mathrm{x}}\:+\mathrm{2}\:\right)^{\mathrm{2}\:} \:\right\} \\ $$$$\:\:\: \\ $$$$\:\:\:−\:\:\int\:\:\frac{\mathrm{3}\boldsymbol{\mathrm{x}}\:\boldsymbol{\mathrm{dx}}}{\left(\:\boldsymbol{\mathrm{x}}\:+\mathrm{2}\:\right)^{\mathrm{2}} \:+\mathrm{3}\:\:\:} \\ $$$$\:\:\: \\ $$$$\:\:\:\:\:\:\:\boldsymbol{\mathrm{t}}\:\:\:=\:\:\boldsymbol{\mathrm{x}}\:\:+\:\mathrm{2}\:\:\:\:\Rightarrow\:\:\boldsymbol{\mathrm{x}}\:\:=\:\:\boldsymbol{\mathrm{t}}\:\:−\mathrm{2} \\ $$$$\:\:\:\:\:\:\boldsymbol{\mathrm{dt}}\:\:=\:\:\boldsymbol{\mathrm{dx}} \\ $$$$\:\:\: \\ $$$$\:\:\:−\:\:\int\:\:\:\frac{\mathrm{3}\:\left(\:\boldsymbol{\mathrm{t}}−\:\mathrm{2}\:\right)\:\boldsymbol{\mathrm{dt}}}{\boldsymbol{\mathrm{t}}^{\mathrm{2}} \:\:+\mathrm{3}\:} \\ $$$$\:\:\: \\ $$$$\:\:\:−\:\:\frac{\mathrm{3}}{\mathrm{2}}\:\:\int\:\frac{\mathrm{2}\boldsymbol{\mathrm{t}}}{\boldsymbol{\mathrm{t}}^{\mathrm{2}} \:+\mathrm{3}}\:\:+\:\:\mathrm{6}\:\:\int\:\:\frac{\boldsymbol{\mathrm{dt}}}{\boldsymbol{\mathrm{t}}^{\mathrm{2}} \:\:+\mathrm{3}\:} \\ $$$$\:\:\: \\ $$$$\:\:\:\:−\frac{\mathrm{3}}{\mathrm{2}}\:\:\mathrm{ln}\:\:\left(\:\boldsymbol{\mathrm{t}}^{\mathrm{2}} \:+\mathrm{3}\:\right)\:\:+\:\mathrm{6}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:\:\mathrm{tan}^{−\mathrm{1}} \left(\:\frac{\boldsymbol{\mathrm{t}}}{\:\sqrt{\mathrm{3}}}\:\right)\:+\:\boldsymbol{\mathrm{C}} \\ $$$$\:\:\: \\ $$$$\:\:\:−\:\frac{\mathrm{3}}{\mathrm{2}}\:\mathrm{ln}\:\:\left(\:\mathrm{1}−\mathrm{4}\boldsymbol{\mathrm{x}}\:−\boldsymbol{\mathrm{x}}^{\mathrm{2}} \:\right)\:+\:\frac{\mathrm{6}}{\:\sqrt{\mathrm{3}}}\:\mathrm{tan}^{−\mathrm{1}} \left(\:\frac{\boldsymbol{\mathrm{x}}+\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:\right)+\boldsymbol{\mathrm{C}} \\ $$$$\:\: \\ $$$$\:\:\boldsymbol{\mathrm{Haladu}}\:\:\boldsymbol{\mathrm{B}}\:\:\:\:\boldsymbol{\mathrm{Bello}} \\ $$

Commented by MikeH last updated on 23/Apr/22

$$\mathrm{thanks}\:\mathrm{a}\:\mathrm{lot} \\ $$

Commented by MJS_new last updated on 24/Apr/22

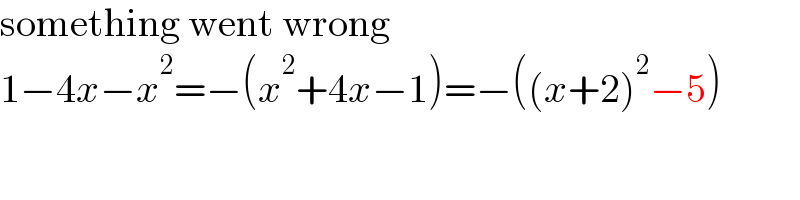
something went wrong 1−4x−x^2 =−(x^2 +4x−1)=−((x+2)^2 −5)

$$\mathrm{something}\:\mathrm{went}\:\mathrm{wrong} \\ $$$$\mathrm{1}−\mathrm{4}{x}−{x}^{\mathrm{2}} =−\left({x}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{1}\right)=−\left(\left({x}+\mathrm{2}\right)^{\mathrm{2}} −\mathrm{5}\right) \\ $$

Answered by MJS_new last updated on 24/Apr/22

−∫((3x)/(x^2 +4x−1))dx= [t=((x+2)/( (√5))) → dx=(√5)dt] =−(3/5)∫((5t−2(√5))/(t^2 −1))dt= =−((3(5−2(√5)))/(10))∫(dt/(t−1))−((3(5+2(√5)))/(10))∫(dt/(t+1))= =−((3(5−2(√5)))/(10))ln (t−1) −((3(5+2(√5)))/(10))ln (t+1) = =−((3(5−2(√5)))/(10))ln ∣x+2−(√5)∣ −((3(5+2(√5)))/(10))ln ∣x+2−(√5)∣ +C

$$−\int\frac{\mathrm{3}{x}}{{x}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{1}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{{x}+\mathrm{2}}{\:\sqrt{\mathrm{5}}}\:\rightarrow\:{dx}=\sqrt{\mathrm{5}}{dt}\right] \\ $$$$=−\frac{\mathrm{3}}{\mathrm{5}}\int\frac{\mathrm{5}{t}−\mathrm{2}\sqrt{\mathrm{5}}}{{t}^{\mathrm{2}} −\mathrm{1}}{dt}= \\ $$$$=−\frac{\mathrm{3}\left(\mathrm{5}−\mathrm{2}\sqrt{\mathrm{5}}\right)}{\mathrm{10}}\int\frac{{dt}}{{t}−\mathrm{1}}−\frac{\mathrm{3}\left(\mathrm{5}+\mathrm{2}\sqrt{\mathrm{5}}\right)}{\mathrm{10}}\int\frac{{dt}}{{t}+\mathrm{1}}= \\ $$$$=−\frac{\mathrm{3}\left(\mathrm{5}−\mathrm{2}\sqrt{\mathrm{5}}\right)}{\mathrm{10}}\mathrm{ln}\:\left({t}−\mathrm{1}\right)\:−\frac{\mathrm{3}\left(\mathrm{5}+\mathrm{2}\sqrt{\mathrm{5}}\right)}{\mathrm{10}}\mathrm{ln}\:\left({t}+\mathrm{1}\right)\:= \\ $$$$=−\frac{\mathrm{3}\left(\mathrm{5}−\mathrm{2}\sqrt{\mathrm{5}}\right)}{\mathrm{10}}\mathrm{ln}\:\mid{x}+\mathrm{2}−\sqrt{\mathrm{5}}\mid\:−\frac{\mathrm{3}\left(\mathrm{5}+\mathrm{2}\sqrt{\mathrm{5}}\right)}{\mathrm{10}}\mathrm{ln}\:\mid{x}+\mathrm{2}−\sqrt{\mathrm{5}}\mid\:+{C} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply