Question Number 46977 by 23kpratik last updated on 03/Nov/18
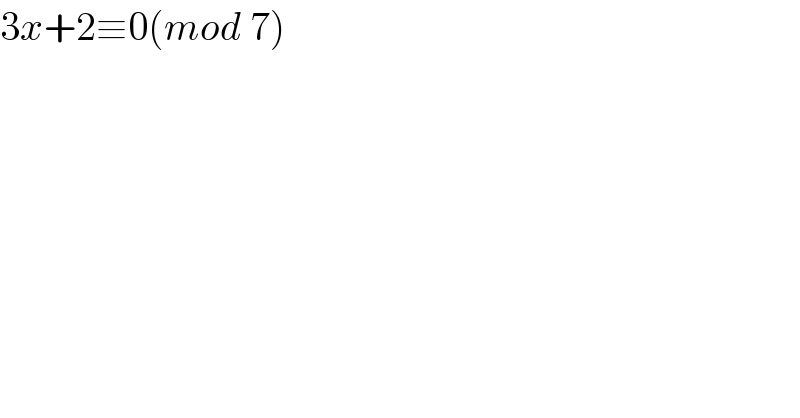
$$\mathrm{3}{x}+\mathrm{2}\equiv\mathrm{0}\left({mod}\:\mathrm{7}\right) \\ $$
Commented by maxmathsup by imad last updated on 03/Nov/18
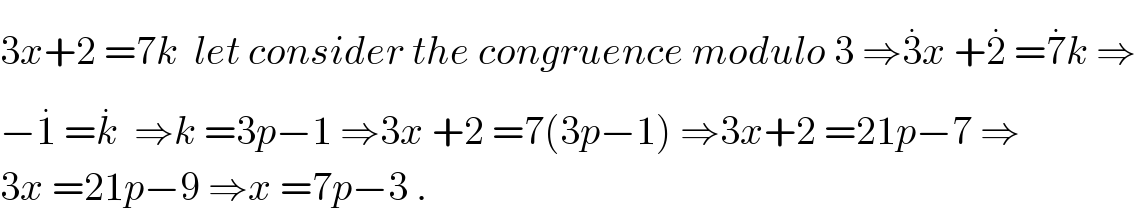
$$\mathrm{3}{x}+\mathrm{2}\:=\mathrm{7}{k}\:\:{let}\:{consider}\:{the}\:{congruence}\:{modulo}\:\mathrm{3}\:\Rightarrow\overset{.} {\mathrm{3}}{x}\:+\overset{.} {\mathrm{2}}\:=\overset{.} {\mathrm{7}}{k}\:\Rightarrow \\ $$$$−\overset{.} {\mathrm{1}}\:=\overset{.} {{k}}\:\:\Rightarrow{k}\:=\mathrm{3}{p}−\mathrm{1}\:\Rightarrow\mathrm{3}{x}\:+\mathrm{2}\:=\mathrm{7}\left(\mathrm{3}{p}−\mathrm{1}\right)\:\Rightarrow\mathrm{3}{x}+\mathrm{2}\:=\mathrm{21}{p}−\mathrm{7}\:\Rightarrow \\ $$$$\mathrm{3}{x}\:=\mathrm{21}{p}−\mathrm{9}\:\Rightarrow{x}\:=\mathrm{7}{p}−\mathrm{3}\:. \\ $$
