Question Number 37179 by rahul 19 last updated on 10/Jun/18
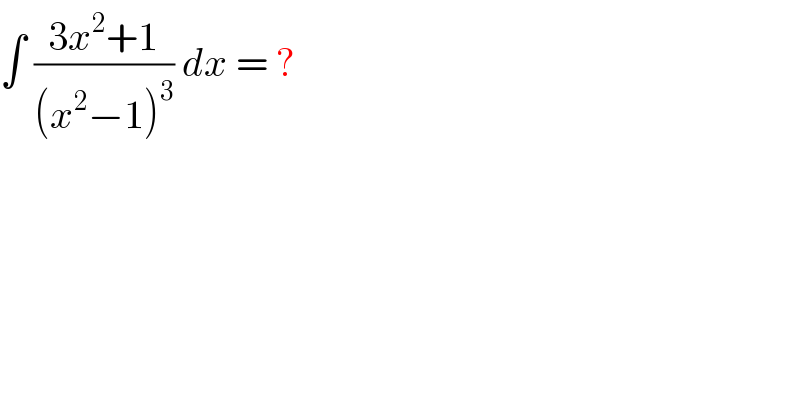
$$\int\:\frac{\mathrm{3}{x}^{\mathrm{2}} +\mathrm{1}}{\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{3}} }\:{dx}\:=\:? \\ $$
Commented by rahul 19 last updated on 10/Jun/18

$$\mathrm{ok}\:\mathrm{sir}. \\ $$
Commented by rahul 19 last updated on 10/Jun/18

$$\mathrm{I}\:\mathrm{hve}\:\mathrm{done}\:\mathrm{this}\:\mathrm{by}\:\mathrm{partial}\:\mathrm{fractions} \\ $$$$\mathrm{but}\:\mathrm{it}'\mathrm{s}\:\mathrm{very}\:\mathrm{lengthy}.\:\mathrm{Someone}\:\mathrm{pls} \\ $$$$\mathrm{explain}\:\mathrm{step}\:\mathrm{5}\:\mathrm{in}\:\mathrm{pic}.\:\mathrm{given}\:\mathrm{below}: \\ $$
Commented by rahul 19 last updated on 10/Jun/18

Commented by prakash jain last updated on 10/Jun/18
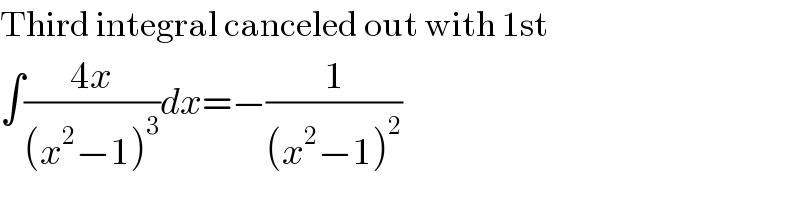
$$\mathrm{Third}\:\mathrm{integral}\:\mathrm{canceled}\:\mathrm{out}\:\mathrm{with}\:\mathrm{1st} \\ $$$$\int\frac{\mathrm{4}{x}}{\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{3}} }{dx}=−\frac{\mathrm{1}}{\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} } \\ $$
