Question Number 128432 by bemath last updated on 07/Jan/21
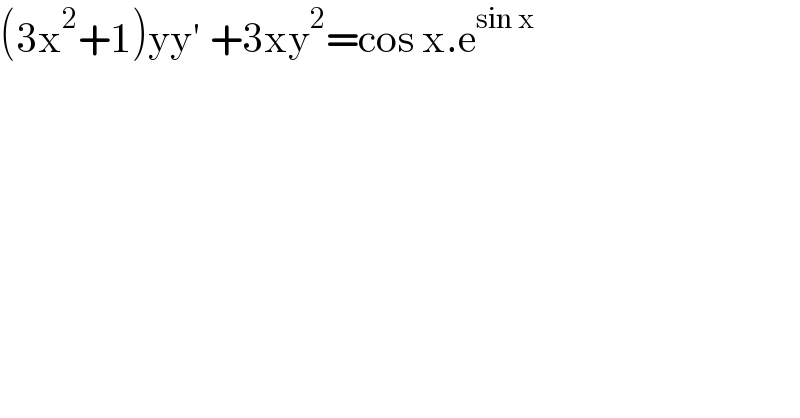
$$\left(\mathrm{3x}^{\mathrm{2}} +\mathrm{1}\right)\mathrm{yy}'\:+\mathrm{3xy}^{\mathrm{2}} =\mathrm{cos}\:\mathrm{x}.\mathrm{e}^{\mathrm{sin}\:\mathrm{x}} \: \\ $$
Answered by liberty last updated on 07/Jan/21
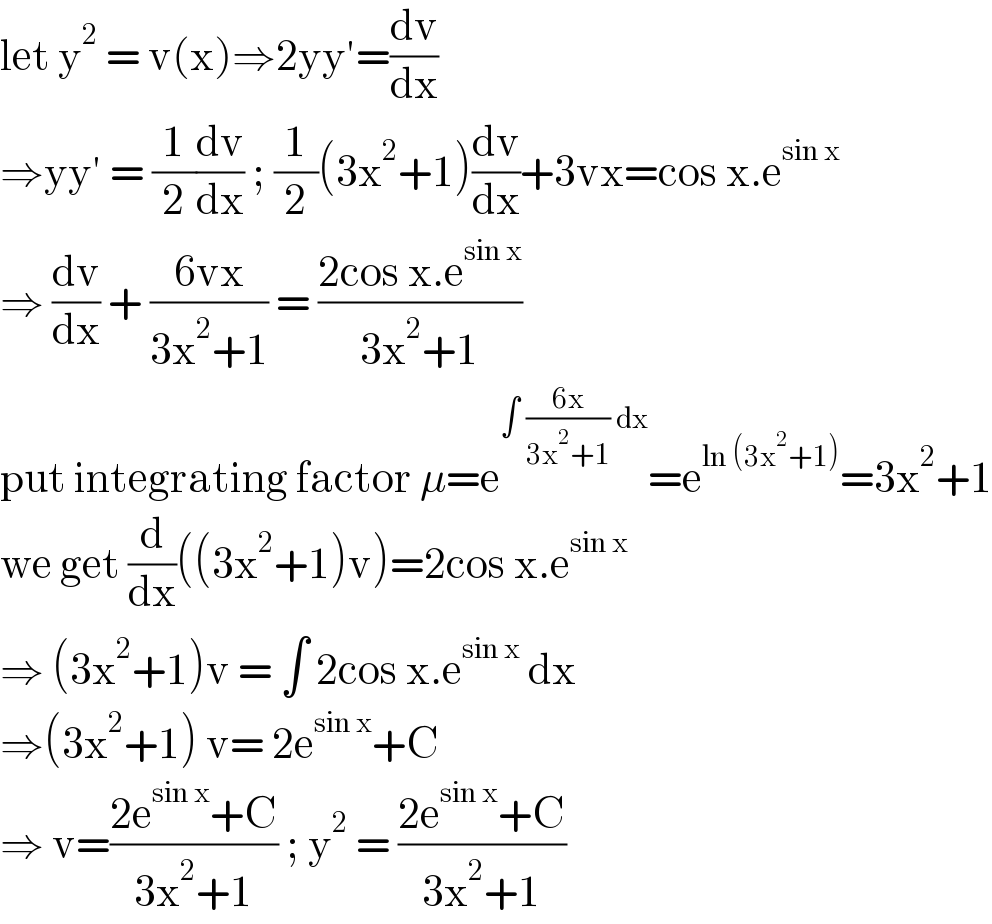
$$\mathrm{let}\:\mathrm{y}^{\mathrm{2}} \:=\:\mathrm{v}\left(\mathrm{x}\right)\Rightarrow\mathrm{2yy}'=\frac{\mathrm{dv}}{\mathrm{dx}} \\ $$$$\Rightarrow\mathrm{yy}'\:=\:\frac{\mathrm{1}}{\mathrm{2}}\frac{\mathrm{dv}}{\mathrm{dx}}\:;\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3x}^{\mathrm{2}} +\mathrm{1}\right)\frac{\mathrm{dv}}{\mathrm{dx}}+\mathrm{3vx}=\mathrm{cos}\:\mathrm{x}.\mathrm{e}^{\mathrm{sin}\:\mathrm{x}} \\ $$$$\Rightarrow\:\frac{\mathrm{dv}}{\mathrm{dx}}\:+\:\frac{\mathrm{6vx}}{\mathrm{3x}^{\mathrm{2}} +\mathrm{1}}\:=\:\frac{\mathrm{2cos}\:\mathrm{x}.\mathrm{e}^{\mathrm{sin}\:\mathrm{x}} }{\mathrm{3x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\mathrm{put}\:\mathrm{integrating}\:\mathrm{factor}\:\mu=\mathrm{e}^{\int\:\frac{\mathrm{6x}}{\mathrm{3x}^{\mathrm{2}} +\mathrm{1}}\:\mathrm{dx}} =\mathrm{e}^{\mathrm{ln}\:\left(\mathrm{3x}^{\mathrm{2}} +\mathrm{1}\right)} =\mathrm{3x}^{\mathrm{2}} +\mathrm{1} \\ $$$$\mathrm{we}\:\mathrm{get}\:\frac{\mathrm{d}}{\mathrm{dx}}\left(\left(\mathrm{3x}^{\mathrm{2}} +\mathrm{1}\right)\mathrm{v}\right)=\mathrm{2cos}\:\mathrm{x}.\mathrm{e}^{\mathrm{sin}\:\mathrm{x}} \\ $$$$\Rightarrow\:\left(\mathrm{3x}^{\mathrm{2}} +\mathrm{1}\right)\mathrm{v}\:=\:\int\:\mathrm{2cos}\:\mathrm{x}.\mathrm{e}^{\mathrm{sin}\:\mathrm{x}} \:\mathrm{dx} \\ $$$$\Rightarrow\left(\mathrm{3x}^{\mathrm{2}} +\mathrm{1}\right)\:\mathrm{v}=\:\mathrm{2e}^{\mathrm{sin}\:\mathrm{x}} +\mathrm{C} \\ $$$$\Rightarrow\:\mathrm{v}=\frac{\mathrm{2e}^{\mathrm{sin}\:\mathrm{x}} +\mathrm{C}}{\mathrm{3x}^{\mathrm{2}} +\mathrm{1}}\:;\:\mathrm{y}^{\mathrm{2}} \:=\:\frac{\mathrm{2e}^{\mathrm{sin}\:\mathrm{x}} +\mathrm{C}}{\mathrm{3x}^{\mathrm{2}} +\mathrm{1}} \\ $$
