Question Number 32785 by NECx last updated on 02/Apr/18
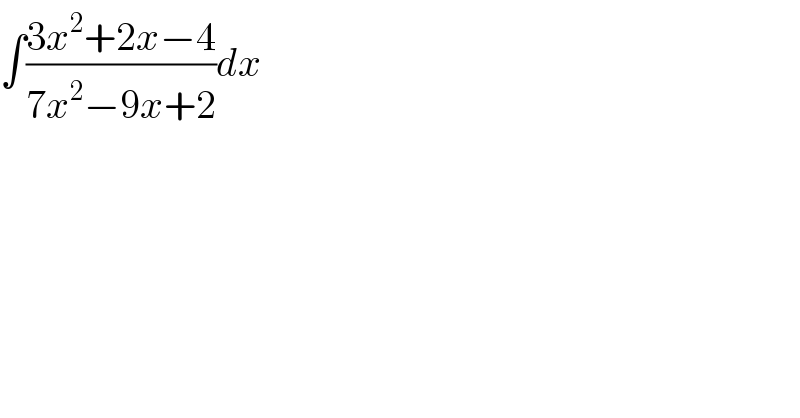
$$\int\frac{\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{4}}{\mathrm{7}{x}^{\mathrm{2}} −\mathrm{9}{x}+\mathrm{2}}{dx} \\ $$
Answered by Joel578 last updated on 02/Apr/18
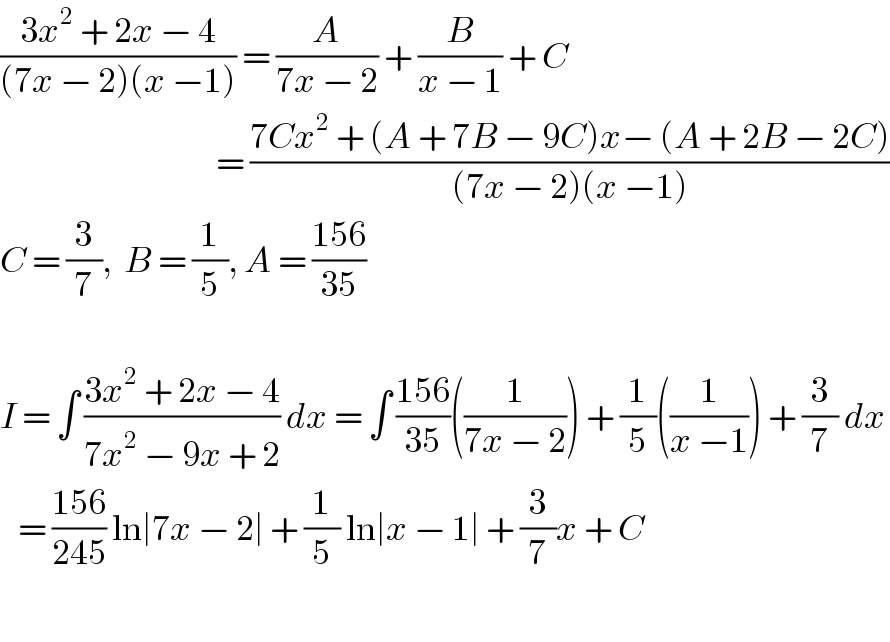
$$\frac{\mathrm{3}{x}^{\mathrm{2}} \:+\:\mathrm{2}{x}\:−\:\mathrm{4}}{\left(\mathrm{7}{x}\:−\:\mathrm{2}\right)\left({x}\:−\mathrm{1}\right)}\:=\:\frac{{A}}{\mathrm{7}{x}\:−\:\mathrm{2}}\:+\:\frac{{B}}{{x}\:−\:\mathrm{1}}\:+\:{C} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{7}{Cx}^{\mathrm{2}} \:+\:\left({A}\:+\:\mathrm{7}{B}\:−\:\mathrm{9}{C}\right){x}−\:\left({A}\:+\:\mathrm{2}{B}\:−\:\mathrm{2}{C}\right)}{\left(\mathrm{7}{x}\:−\:\mathrm{2}\right)\left({x}\:−\mathrm{1}\right)} \\ $$$${C}\:=\:\frac{\mathrm{3}}{\mathrm{7}},\:\:{B}\:=\:\frac{\mathrm{1}}{\mathrm{5}},\:{A}\:=\:\frac{\mathrm{156}}{\mathrm{35}} \\ $$$$ \\ $$$${I}\:=\:\int\:\frac{\mathrm{3}{x}^{\mathrm{2}} \:+\:\mathrm{2}{x}\:−\:\mathrm{4}}{\mathrm{7}{x}^{\mathrm{2}} \:−\:\mathrm{9}{x}\:+\:\mathrm{2}}\:{dx}\:=\:\int\:\frac{\mathrm{156}}{\mathrm{35}}\left(\frac{\mathrm{1}}{\mathrm{7}{x}\:−\:\mathrm{2}}\right)\:+\:\frac{\mathrm{1}}{\mathrm{5}}\left(\frac{\mathrm{1}}{{x}\:−\mathrm{1}}\right)\:+\:\frac{\mathrm{3}}{\mathrm{7}}\:{dx} \\ $$$$\:\:\:=\:\frac{\mathrm{156}}{\mathrm{245}}\:\mathrm{ln}\mid\mathrm{7}{x}\:−\:\mathrm{2}\mid\:+\:\frac{\mathrm{1}}{\mathrm{5}}\:\mathrm{ln}\mid{x}\:−\:\mathrm{1}\mid\:+\:\frac{\mathrm{3}}{\mathrm{7}}{x}\:+\:{C}\: \\ $$$$ \\ $$
