3x-2-2x-dx-

Question Number 107567 by Ar Brandon last updated on 11/Aug/20

$$\int\sqrt{\mathrm{3x}^{\mathrm{2}} −\mathrm{2x}}\:\mathrm{dx} \\ $$

Answered by bobhans last updated on 11/Aug/20

∫ (√(3x^2 −2x)) dx = ∫(√(3(x^2 −((2x)/3)+(1/9))−(1/3))) dx =(√3) ∫(√((x−(1/3))^2 −((1/( (√3))))^2 )) dx set x−(1/3) = (1/( (√3))) sec θ =(√3) ∫(√((1/3)tan^2 θ)) (1/( (√3))) sec θ tan θ dθ = ((√3)/3)∫ tan^2 θ sec θ dθ = ((√3)/3)∫(sec^3 θ−sec θ)dθ note ∫ sec^3 x dx = ((sin x)/(2cos^2 x))+(1/2)ln ∣tan(x+(π/4))∣+c =(1/2)tan x sec x +(1/2)ln ∣((1+tan x)/(1−tan x))∣+c and ∫ sec x dx = ln ∣sec x+tan x∣ +c

$$\int\:\sqrt{\mathrm{3x}^{\mathrm{2}} −\mathrm{2x}}\:\mathrm{dx}\:=\:\int\sqrt{\mathrm{3}\left(\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{2x}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{9}}\right)−\frac{\mathrm{1}}{\mathrm{3}}}\:\mathrm{dx} \\ $$$$=\sqrt{\mathrm{3}}\:\int\sqrt{\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} }\:\mathrm{dx}\: \\ $$$$\mathrm{set}\:\mathrm{x}−\frac{\mathrm{1}}{\mathrm{3}}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:\mathrm{sec}\:\theta\: \\ $$$$=\sqrt{\mathrm{3}}\:\int\sqrt{\frac{\mathrm{1}}{\mathrm{3}}\mathrm{tan}\:^{\mathrm{2}} \theta}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:\mathrm{sec}\:\theta\:\mathrm{tan}\:\theta\:\mathrm{d}\theta \\ $$$$=\:\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\int\:\mathrm{tan}\:^{\mathrm{2}} \theta\:\mathrm{sec}\:\theta\:\mathrm{d}\theta\:=\:\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\int\left(\mathrm{sec}\:^{\mathrm{3}} \theta−\mathrm{sec}\:\theta\right)\mathrm{d}\theta \\ $$$$\mathrm{note}\:\int\:\mathrm{sec}\:^{\mathrm{3}} \:\mathrm{x}\:\mathrm{dx}\:=\:\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{2cos}\:^{\mathrm{2}} \mathrm{x}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid\mathrm{tan}\left(\mathrm{x}+\frac{\pi}{\mathrm{4}}\right)\mid+\mathrm{c} \\ $$$$\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}\:\mathrm{x}\:\mathrm{sec}\:\mathrm{x}\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid\frac{\mathrm{1}+\mathrm{tan}\:\mathrm{x}}{\mathrm{1}−\mathrm{tan}\:\mathrm{x}}\mid+\mathrm{c} \\ $$$$\mathrm{and}\:\int\:\mathrm{sec}\:\mathrm{x}\:\mathrm{dx}\:=\:\mathrm{ln}\:\mid\mathrm{sec}\:\mathrm{x}+\mathrm{tan}\:\mathrm{x}\mid\:+\mathrm{c}\: \\ $$$$ \\ $$

Commented by Ar Brandon last updated on 11/Aug/20

Thanks Sir.��

Commented by bobhans last updated on 12/Aug/20

��

Answered by mathmax by abdo last updated on 11/Aug/20

I =∫(√(3(x^2 −(2/3)x)))dx =(√3)∫(√(x^2 −(2/3)x +(1/9)−(1/9)))dx =(√3)∫(√((x−(1/3))^2 −(1/9)))dx =_(x−(1/3)=(1/3)ch(t)) (√3)∫ (1/3) sht .(1/3)sh(t)dt =((√3)/9) ∫sh^2 t dt =((√3)/9) ∫ ((ch(2t)−1)/2)dt =((√3)/(18)) ∫ch(2t)dt−((√3)/(18))t =((√3)/(36))sh(2t) −((√3)/(18))t +C =((√3)/(18))ch(t)sh(t)−((√3)/(18))t +C =((√3)/(18))(3x−1)(√((3x−1)^2 −1))−((√3)/(18))argch(3x−1) +C I=((√3)/(18))(3x−1)(√((3x−1)^2 −1)) −((√3)/(18))ln(3x−1+(√((3x−1)^2 −1))) +C

$$\mathrm{I}\:=\int\sqrt{\mathrm{3}\left(\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{2}}{\mathrm{3}}\mathrm{x}\right)}\mathrm{dx}\:=\sqrt{\mathrm{3}}\int\sqrt{\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{2}}{\mathrm{3}}\mathrm{x}\:+\frac{\mathrm{1}}{\mathrm{9}}−\frac{\mathrm{1}}{\mathrm{9}}}\mathrm{dx} \\ $$$$=\sqrt{\mathrm{3}}\int\sqrt{\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{9}}}\mathrm{dx}\:=_{\mathrm{x}−\frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ch}\left(\mathrm{t}\right)} \sqrt{\mathrm{3}}\int\:\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{sht}\:.\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sh}\left(\mathrm{t}\right)\mathrm{dt} \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{9}}\:\int\mathrm{sh}^{\mathrm{2}} \mathrm{t}\:\mathrm{dt}\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{9}}\:\int\:\frac{\mathrm{ch}\left(\mathrm{2t}\right)−\mathrm{1}}{\mathrm{2}}\mathrm{dt}\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{18}}\:\int\mathrm{ch}\left(\mathrm{2t}\right)\mathrm{dt}−\frac{\sqrt{\mathrm{3}}}{\mathrm{18}}\mathrm{t}\: \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{36}}\mathrm{sh}\left(\mathrm{2t}\right)\:−\frac{\sqrt{\mathrm{3}}}{\mathrm{18}}\mathrm{t}\:+\mathrm{C} \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{18}}\mathrm{ch}\left(\mathrm{t}\right)\mathrm{sh}\left(\mathrm{t}\right)−\frac{\sqrt{\mathrm{3}}}{\mathrm{18}}\mathrm{t}\:+\mathrm{C} \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{18}}\left(\mathrm{3x}−\mathrm{1}\right)\sqrt{\left(\mathrm{3x}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{18}}\mathrm{argch}\left(\mathrm{3x}−\mathrm{1}\right)\:+\mathrm{C} \\ $$$$\mathrm{I}=\frac{\sqrt{\mathrm{3}}}{\mathrm{18}}\left(\mathrm{3x}−\mathrm{1}\right)\sqrt{\left(\mathrm{3x}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}}\:−\frac{\sqrt{\mathrm{3}}}{\mathrm{18}}\mathrm{ln}\left(\mathrm{3x}−\mathrm{1}+\sqrt{\left(\mathrm{3x}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}}\right)\:+\mathrm{C} \\ $$

Answered by Dwaipayan Shikari last updated on 12/Aug/20

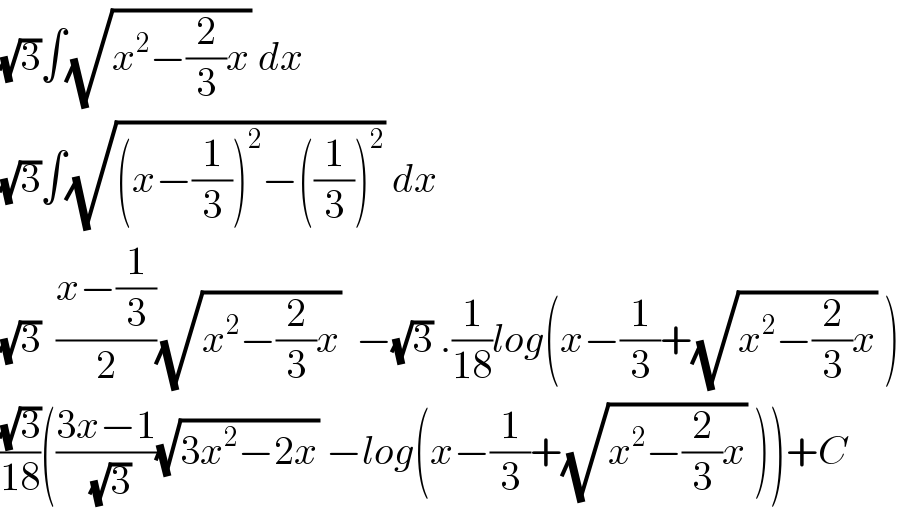
(√3)∫(√(x^2 −(2/3)x)) dx (√3)∫(√((x−(1/3))^2 −((1/3))^2 )) dx (√3) ((x−(1/3))/2)(√(x^2 −(2/3)x)) −(√3) .(1/(18))log(x−(1/3)+(√(x^2 −(2/3)x)) ) ((√3)/(18))(((3x−1)/( (√3)))(√(3x^2 −2x)) −log(x−(1/3)+(√(x^2 −(2/3)x)) ))+C

$$\sqrt{\mathrm{3}}\int\sqrt{{x}^{\mathrm{2}} −\frac{\mathrm{2}}{\mathrm{3}}{x}}\:{dx} \\ $$$$\sqrt{\mathrm{3}}\int\sqrt{\left({x}−\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} }\:{dx} \\ $$$$\sqrt{\mathrm{3}}\:\:\frac{{x}−\frac{\mathrm{1}}{\mathrm{3}}}{\mathrm{2}}\sqrt{{x}^{\mathrm{2}} −\frac{\mathrm{2}}{\mathrm{3}}{x}}\:\:−\sqrt{\mathrm{3}}\:.\frac{\mathrm{1}}{\mathrm{18}}{log}\left({x}−\frac{\mathrm{1}}{\mathrm{3}}+\sqrt{{x}^{\mathrm{2}} −\frac{\mathrm{2}}{\mathrm{3}}{x}}\:\right) \\ $$$$\frac{\sqrt{\mathrm{3}}}{\mathrm{18}}\left(\frac{\mathrm{3}{x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\sqrt{\mathrm{3}{x}^{\mathrm{2}} −\mathrm{2}{x}}\:−{log}\left({x}−\frac{\mathrm{1}}{\mathrm{3}}+\sqrt{{x}^{\mathrm{2}} −\frac{\mathrm{2}}{\mathrm{3}}{x}}\:\right)\right)+{C} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply