Question Number 152034 by mathdanisur last updated on 25/Aug/21
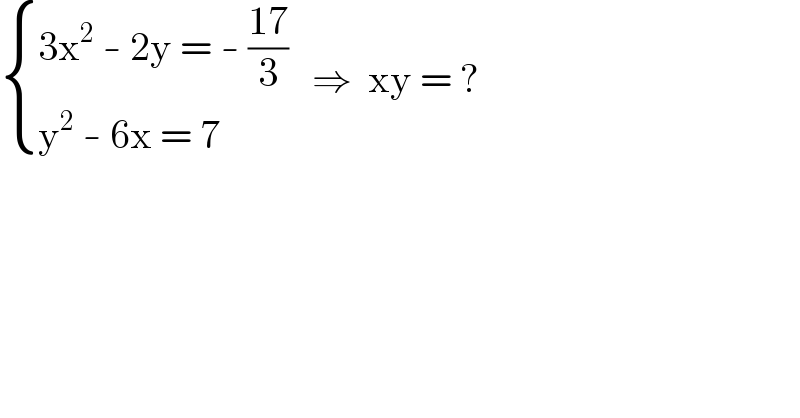
$$\begin{cases}{\mathrm{3x}^{\mathrm{2}} \:-\:\mathrm{2y}\:=\:-\:\frac{\mathrm{17}}{\mathrm{3}}}\\{\mathrm{y}^{\mathrm{2}} \:-\:\mathrm{6x}\:=\:\mathrm{7}}\end{cases}\:\:\:\Rightarrow\:\:\mathrm{xy}\:=\:? \\ $$
Answered by Rasheed.Sindhi last updated on 25/Aug/21
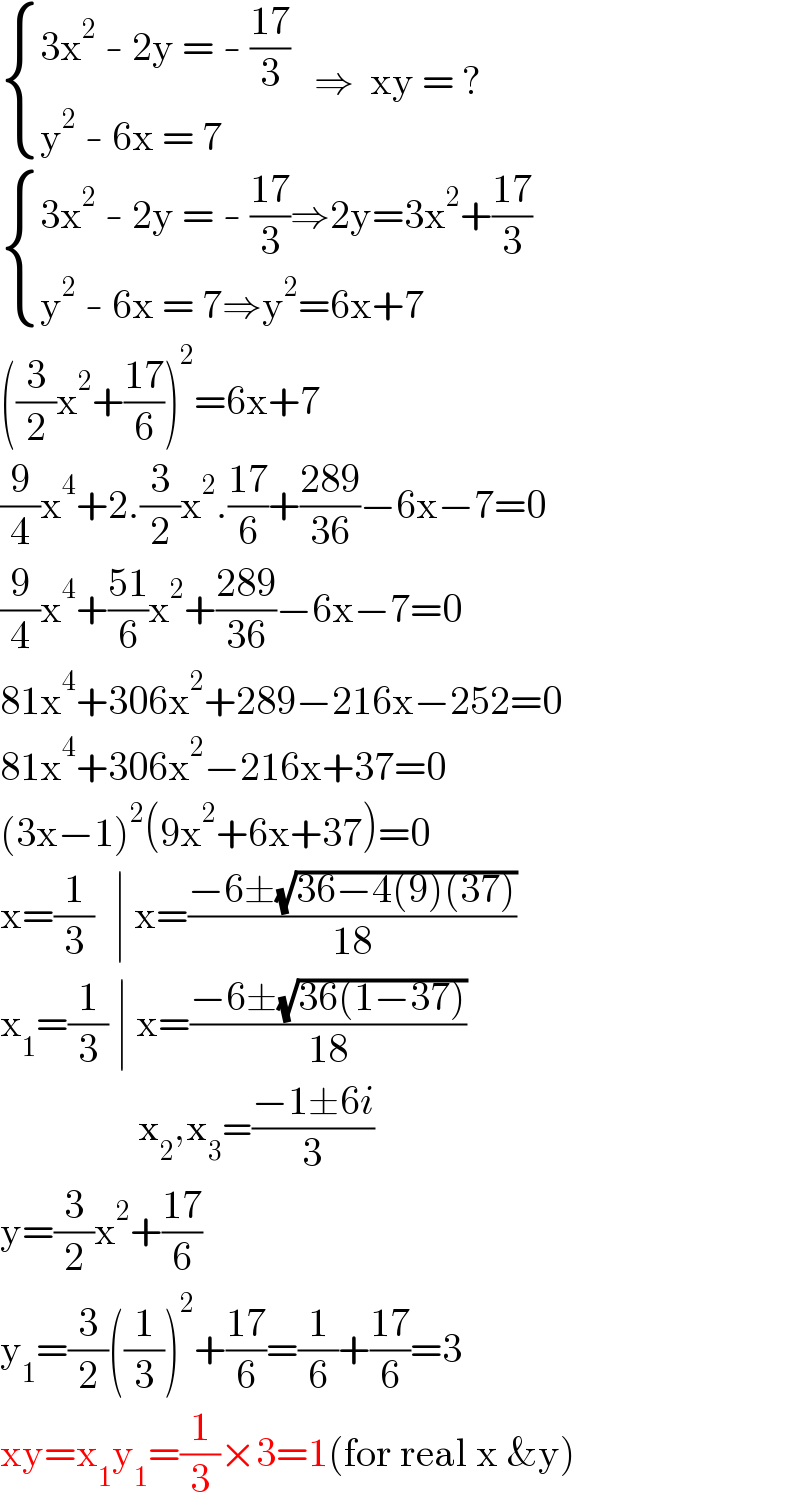
$$\begin{cases}{\mathrm{3x}^{\mathrm{2}} \:-\:\mathrm{2y}\:=\:-\:\frac{\mathrm{17}}{\mathrm{3}}}\\{\mathrm{y}^{\mathrm{2}} \:-\:\mathrm{6x}\:=\:\mathrm{7}}\end{cases}\:\:\:\Rightarrow\:\:\mathrm{xy}\:=\:?\: \\ $$$$\begin{cases}{\mathrm{3x}^{\mathrm{2}} \:-\:\mathrm{2y}\:=\:-\:\frac{\mathrm{17}}{\mathrm{3}}\Rightarrow\mathrm{2y}=\mathrm{3x}^{\mathrm{2}} +\frac{\mathrm{17}}{\mathrm{3}}}\\{\mathrm{y}^{\mathrm{2}} \:-\:\mathrm{6x}\:=\:\mathrm{7}\Rightarrow\mathrm{y}^{\mathrm{2}} =\mathrm{6x}+\mathrm{7}}\end{cases}\:\:\:\: \\ $$$$\left(\frac{\mathrm{3}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{17}}{\mathrm{6}}\right)^{\mathrm{2}} =\mathrm{6x}+\mathrm{7} \\ $$$$\frac{\mathrm{9}}{\mathrm{4}}\mathrm{x}^{\mathrm{4}} +\mathrm{2}.\frac{\mathrm{3}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} .\frac{\mathrm{17}}{\mathrm{6}}+\frac{\mathrm{289}}{\mathrm{36}}−\mathrm{6x}−\mathrm{7}=\mathrm{0} \\ $$$$\frac{\mathrm{9}}{\mathrm{4}}\mathrm{x}^{\mathrm{4}} +\frac{\mathrm{51}}{\mathrm{6}}\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{289}}{\mathrm{36}}−\mathrm{6x}−\mathrm{7}=\mathrm{0} \\ $$$$\mathrm{81x}^{\mathrm{4}} +\mathrm{306x}^{\mathrm{2}} +\mathrm{289}−\mathrm{216x}−\mathrm{252}=\mathrm{0} \\ $$$$\mathrm{81x}^{\mathrm{4}} +\mathrm{306x}^{\mathrm{2}} −\mathrm{216x}+\mathrm{37}=\mathrm{0} \\ $$$$\left(\mathrm{3x}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{9x}^{\mathrm{2}} +\mathrm{6x}+\mathrm{37}\right)=\mathrm{0} \\ $$$$\mathrm{x}=\frac{\mathrm{1}}{\mathrm{3}}\:\:\:\mid\:\mathrm{x}=\frac{−\mathrm{6}\pm\sqrt{\mathrm{36}−\mathrm{4}\left(\mathrm{9}\right)\left(\mathrm{37}\right)}}{\mathrm{18}} \\ $$$$\mathrm{x}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{3}}\:\mid\:\mathrm{x}=\frac{−\mathrm{6}\pm\sqrt{\mathrm{36}\left(\mathrm{1}−\mathrm{37}\right)}}{\mathrm{18}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}_{\mathrm{2}} ,\mathrm{x}_{\mathrm{3}} =\frac{−\mathrm{1}\pm\mathrm{6}{i}}{\mathrm{3}} \\ $$$$\mathrm{y}=\frac{\mathrm{3}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{17}}{\mathrm{6}} \\ $$$$\mathrm{y}_{\mathrm{1}} =\frac{\mathrm{3}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} +\frac{\mathrm{17}}{\mathrm{6}}=\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{17}}{\mathrm{6}}=\mathrm{3} \\ $$$$\mathrm{xy}=\mathrm{x}_{\mathrm{1}} \mathrm{y}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{3}}×\mathrm{3}=\mathrm{1}\left(\mathrm{for}\:\mathrm{real}\:\mathrm{x}\:\&\mathrm{y}\right) \\ $$
Commented by mathdanisur last updated on 25/Aug/21

$$\mathrm{Thank}\:\mathrm{You}\:\boldsymbol{\mathrm{S}}\mathrm{er} \\ $$
Answered by john_santu last updated on 25/Aug/21
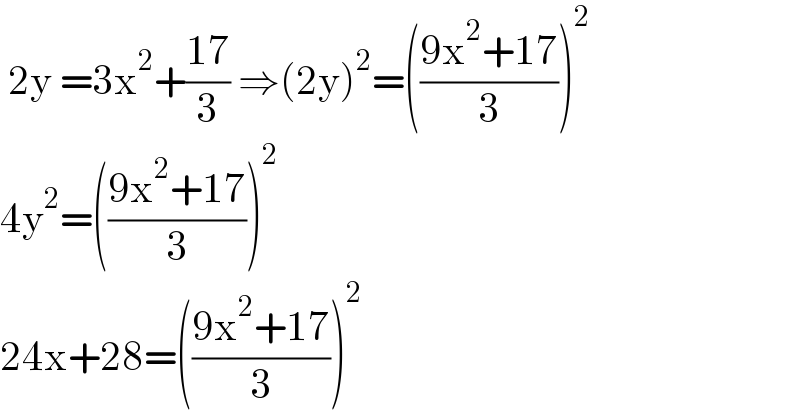
$$\:\mathrm{2y}\:=\mathrm{3x}^{\mathrm{2}} +\frac{\mathrm{17}}{\mathrm{3}}\:\Rightarrow\left(\mathrm{2y}\right)^{\mathrm{2}} =\left(\frac{\mathrm{9x}^{\mathrm{2}} +\mathrm{17}}{\mathrm{3}}\right)^{\mathrm{2}} \\ $$$$\mathrm{4y}^{\mathrm{2}} =\left(\frac{\mathrm{9x}^{\mathrm{2}} +\mathrm{17}}{\mathrm{3}}\right)^{\mathrm{2}} \\ $$$$\mathrm{24x}+\mathrm{28}=\left(\frac{\mathrm{9x}^{\mathrm{2}} +\mathrm{17}}{\mathrm{3}}\right)^{\mathrm{2}} \\ $$
