Question Number 95262 by 6532 last updated on 24/May/20
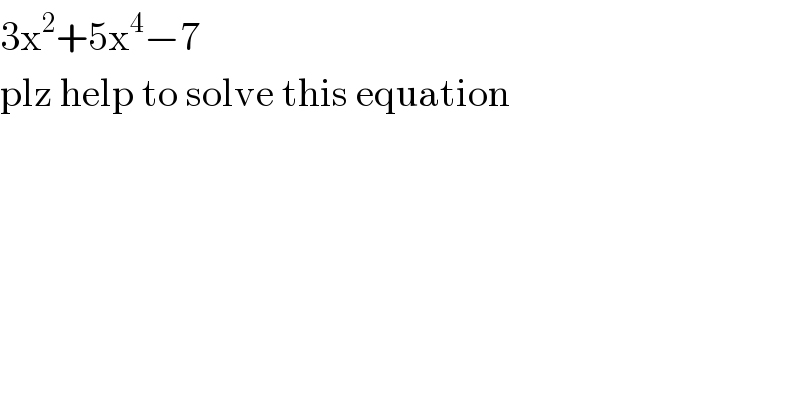
$$\mathrm{3x}^{\mathrm{2}} +\mathrm{5x}^{\mathrm{4}} −\mathrm{7} \\ $$$$\mathrm{plz}\:\mathrm{help}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{this}\:\mathrm{equation} \\ $$
Answered by i jagooll last updated on 24/May/20
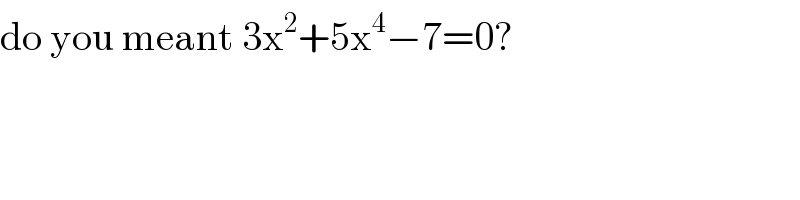
$$\mathrm{do}\:\mathrm{you}\:\mathrm{meant}\:\mathrm{3x}^{\mathrm{2}} +\mathrm{5x}^{\mathrm{4}} −\mathrm{7}=\mathrm{0}? \\ $$
Commented by 6532 last updated on 24/May/20
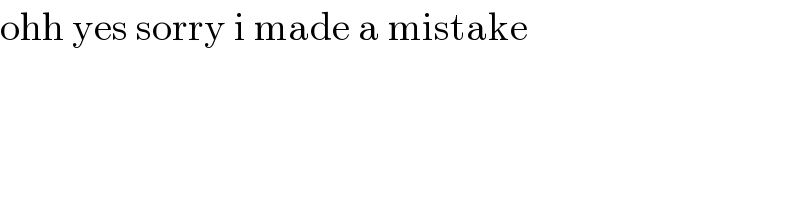
$$\mathrm{ohh}\:\mathrm{yes}\:\mathrm{sorry}\:\mathrm{i}\:\mathrm{made}\:\mathrm{a}\:\mathrm{mistake} \\ $$
Answered by bobhans last updated on 24/May/20
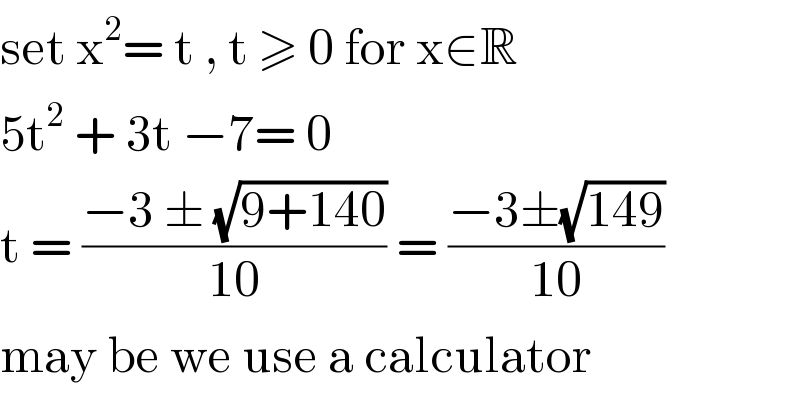
$$\mathrm{set}\:\mathrm{x}^{\mathrm{2}} =\:\mathrm{t}\:,\:\mathrm{t}\:\geqslant\:\mathrm{0}\:\mathrm{for}\:\mathrm{x}\in\mathbb{R} \\ $$$$\mathrm{5t}^{\mathrm{2}} \:+\:\mathrm{3t}\:−\mathrm{7}=\:\mathrm{0} \\ $$$$\mathrm{t}\:=\:\frac{−\mathrm{3}\:\pm\:\sqrt{\mathrm{9}+\mathrm{140}}}{\mathrm{10}}\:=\:\frac{−\mathrm{3}\pm\sqrt{\mathrm{149}}}{\mathrm{10}}\: \\ $$$$\mathrm{may}\:\mathrm{be}\:\mathrm{we}\:\mathrm{use}\:\mathrm{a}\:\mathrm{calculator}\: \\ $$
Answered by MJS last updated on 24/May/20
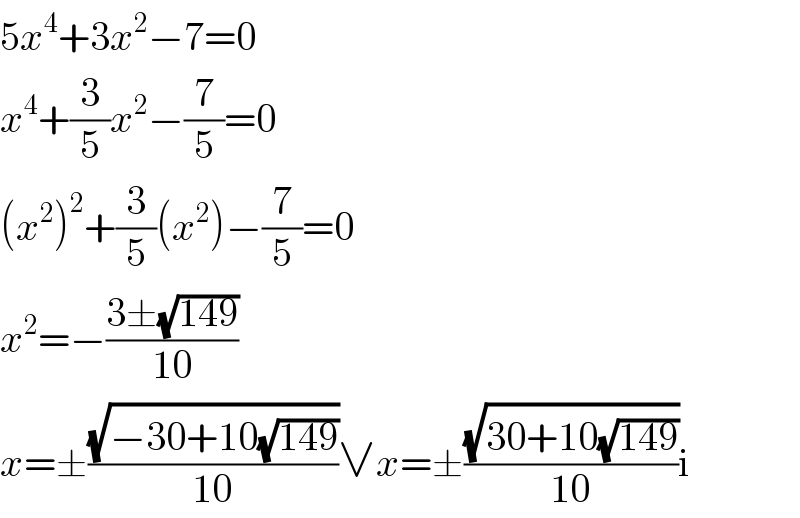
$$\mathrm{5}{x}^{\mathrm{4}} +\mathrm{3}{x}^{\mathrm{2}} −\mathrm{7}=\mathrm{0} \\ $$$${x}^{\mathrm{4}} +\frac{\mathrm{3}}{\mathrm{5}}{x}^{\mathrm{2}} −\frac{\mathrm{7}}{\mathrm{5}}=\mathrm{0} \\ $$$$\left({x}^{\mathrm{2}} \right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{5}}\left({x}^{\mathrm{2}} \right)−\frac{\mathrm{7}}{\mathrm{5}}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} =−\frac{\mathrm{3}\pm\sqrt{\mathrm{149}}}{\mathrm{10}} \\ $$$${x}=\pm\frac{\sqrt{−\mathrm{30}+\mathrm{10}\sqrt{\mathrm{149}}}}{\mathrm{10}}\vee{x}=\pm\frac{\sqrt{\mathrm{30}+\mathrm{10}\sqrt{\mathrm{149}}}}{\mathrm{10}}\mathrm{i} \\ $$
