Question Number 83591 by jagoll last updated on 04/Mar/20
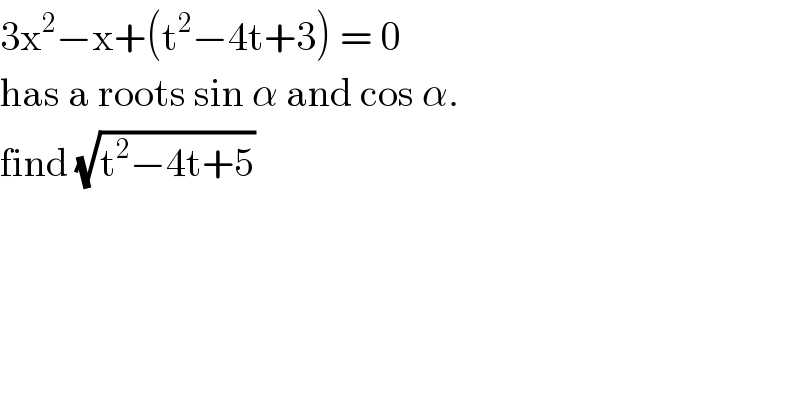
$$\mathrm{3x}^{\mathrm{2}} −\mathrm{x}+\left(\mathrm{t}^{\mathrm{2}} −\mathrm{4t}+\mathrm{3}\right)\:=\:\mathrm{0} \\ $$$$\mathrm{has}\:\mathrm{a}\:\mathrm{roots}\:\mathrm{sin}\:\alpha\:\mathrm{and}\:\mathrm{cos}\:\alpha. \\ $$$$\mathrm{find}\:\sqrt{\mathrm{t}^{\mathrm{2}} −\mathrm{4t}+\mathrm{5}} \\ $$
Commented by jagoll last updated on 04/Mar/20
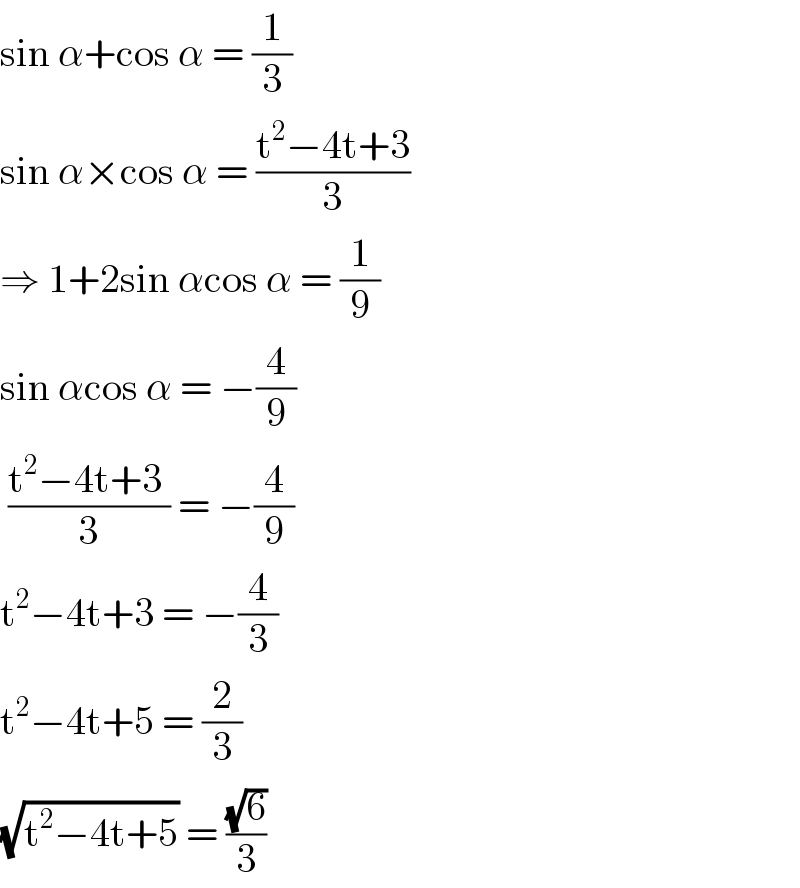
$$\mathrm{sin}\:\alpha+\mathrm{cos}\:\alpha\:=\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{sin}\:\alpha×\mathrm{cos}\:\alpha\:=\:\frac{\mathrm{t}^{\mathrm{2}} −\mathrm{4t}+\mathrm{3}}{\mathrm{3}} \\ $$$$\Rightarrow\:\mathrm{1}+\mathrm{2sin}\:\alpha\mathrm{cos}\:\alpha\:=\:\frac{\mathrm{1}}{\mathrm{9}} \\ $$$$\mathrm{sin}\:\alpha\mathrm{cos}\:\alpha\:=\:−\frac{\mathrm{4}}{\mathrm{9}} \\ $$$$\:\frac{\mathrm{t}^{\mathrm{2}} −\mathrm{4t}+\mathrm{3}\:}{\mathrm{3}}\:=\:−\frac{\mathrm{4}}{\mathrm{9}} \\ $$$$\mathrm{t}^{\mathrm{2}} −\mathrm{4t}+\mathrm{3}\:=\:−\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$\mathrm{t}^{\mathrm{2}} −\mathrm{4t}+\mathrm{5}\:=\:\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\sqrt{\mathrm{t}^{\mathrm{2}} −\mathrm{4t}+\mathrm{5}}\:=\:\frac{\sqrt{\mathrm{6}}}{\mathrm{3}} \\ $$
