Menu Close

3x-3-3x-1-2-0-x-1-x-2-x-3-

Tinku Tara 0 Comments
Pin




Question Number 114263 by Khalmohmmad last updated on 18/Sep/20
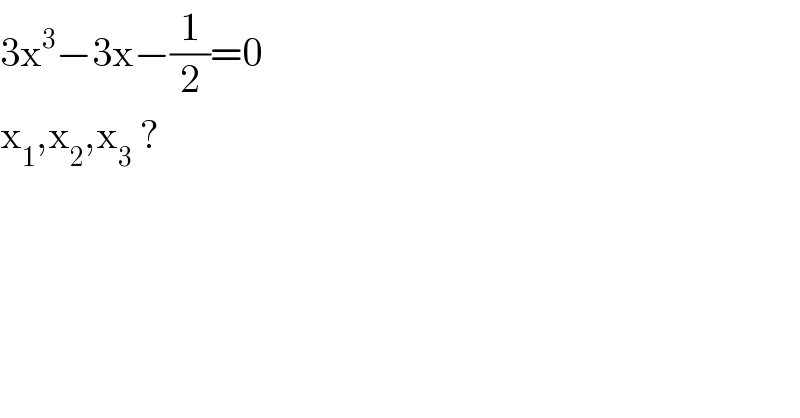
3x^3 −3x−(1/2)=0 x_1 ,x_2 ,x_3 ?
$$\mathrm{3x}^{\mathrm{3}} −\mathrm{3x}−\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{0} \\ $$$$\mathrm{x}_{\mathrm{1}} ,\mathrm{x}_{\mathrm{2}} ,\mathrm{x}_{\mathrm{3}} \:? \\ $$
Answered by MJS_new last updated on 18/Sep/20
x^3 −x−(1/6)=0 p=−1∧q=−(1/6) D=(p^3 /(27))+(q^2 /4)=−((13)/(432))<0 ⇒ trigonometric solution x_(j+1) =((2(√(−3p)))/3)sin (((2πj)/3)+(1/3)arcsin ((3(√3)q)/(2(√(−p^3 )))))) with j=0, 1, 2 in this case x_1 =−((2(√3))/3)sin ((1/3)arcsin ((√3)/4)) ≈−.171731 x_2 =((2(√3))/3)sin ((π/3)+(1/3)arcsin ((√3)/4)) ≈1.07474 x_3 =−((2(√3))/3)cos ((π/6)+(1/3)arcsin ((√3)/4)) ≈−.903013
$${x}^{\mathrm{3}} −{x}−\frac{\mathrm{1}}{\mathrm{6}}=\mathrm{0} \\ $$$${p}=−\mathrm{1}\wedge{q}=−\frac{\mathrm{1}}{\mathrm{6}} \\ $$$${D}=\frac{{p}^{\mathrm{3}} }{\mathrm{27}}+\frac{{q}^{\mathrm{2}} }{\mathrm{4}}=−\frac{\mathrm{13}}{\mathrm{432}}<\mathrm{0}\:\Rightarrow\:\mathrm{trigonometric}\:\mathrm{solution} \\ $$$$\left.{x}_{{j}+\mathrm{1}} =\frac{\mathrm{2}\sqrt{−\mathrm{3}{p}}}{\mathrm{3}}\mathrm{sin}\:\left(\frac{\mathrm{2}\pi{j}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\:\frac{\mathrm{3}\sqrt{\mathrm{3}}{q}}{\mathrm{2}\sqrt{−{p}^{\mathrm{3}} }}\right)\right)\:\mathrm{with}\:{j}=\mathrm{0},\:\mathrm{1},\:\mathrm{2} \\ $$$$\mathrm{in}\:\mathrm{this}\:\mathrm{case} \\ $$$${x}_{\mathrm{1}} =−\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\right)\:\approx−.\mathrm{171731} \\ $$$${x}_{\mathrm{2}} =\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\right)\:\approx\mathrm{1}.\mathrm{07474} \\ $$$${x}_{\mathrm{3}} =−\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{cos}\:\left(\frac{\pi}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\right)\:\approx−.\mathrm{903013} \\ $$
Commented by Khalmohmmad last updated on 19/Sep/20
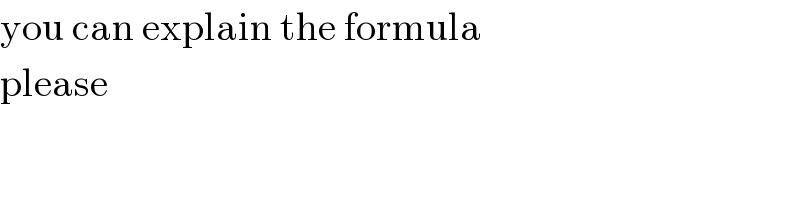
you can explain the formula please
$$\mathrm{you}\:\mathrm{can}\:\mathrm{explain}\:\mathrm{the}\:\mathrm{formula} \\ $$$$\mathrm{please} \\ $$
Commented by MJS_new last updated on 19/Sep/20
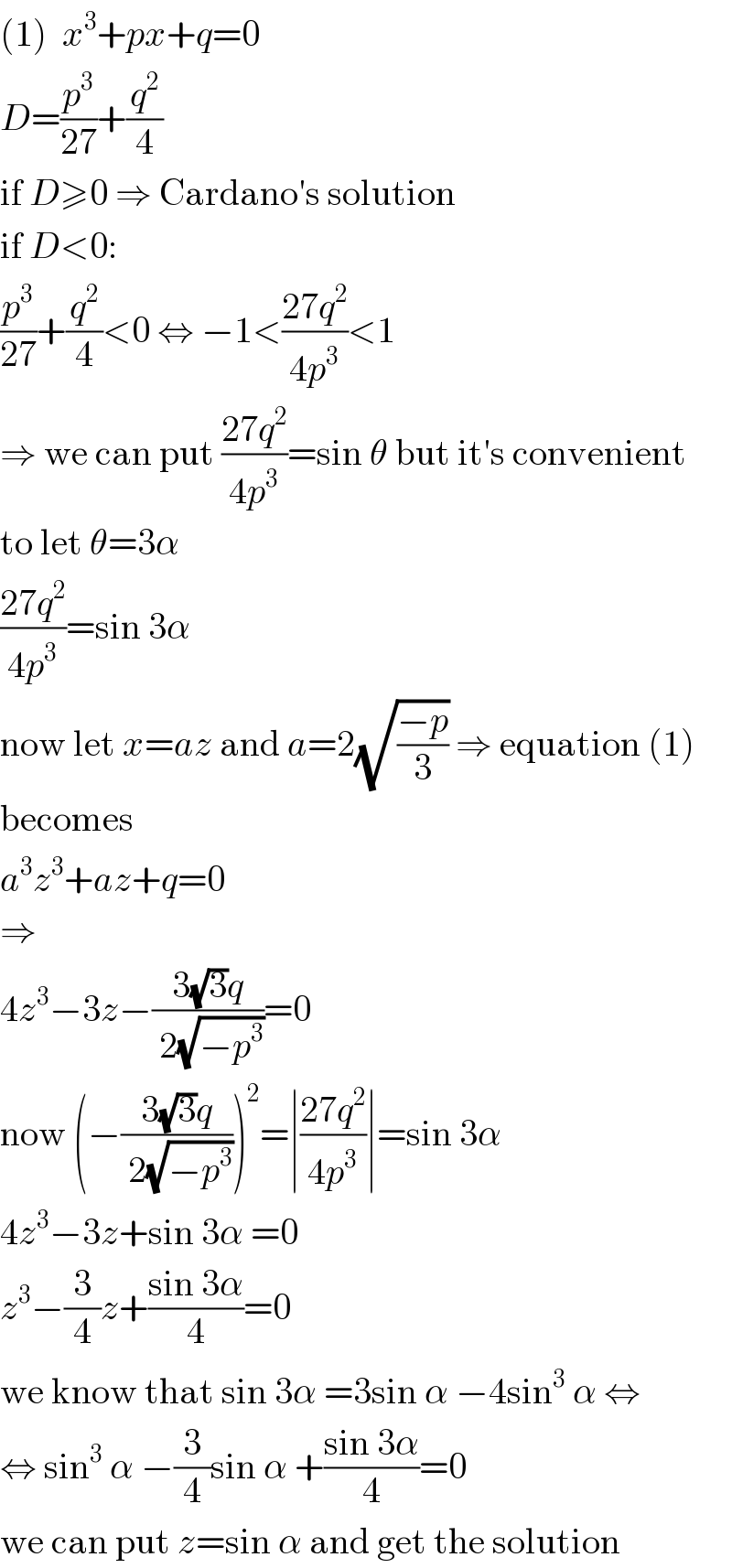
(1) x^3 +px+q=0 D=(p^3 /(27))+(q^2 /4) if D≥0 ⇒ Cardano′s solution if D<0: (p^3 /(27))+(q^2 /4)<0 ⇔ −1<((27q^2 )/(4p^3 ))<1 ⇒ we can put ((27q^2 )/(4p^3 ))=sin θ but it′s convenient to let θ=3α ((27q^2 )/(4p^3 ))=sin 3α now let x=az and a=2(√((−p)/3)) ⇒ equation (1) becomes a^3 z^3 +az+q=0 ⇒ 4z^3 −3z−((3(√3)q)/( 2(√(−p^3 ))))=0 now (−((3(√3)q)/( 2(√(−p^3 )))))^2 =∣((27q^2 )/(4p^3 ))∣=sin 3α 4z^3 −3z+sin 3α =0 z^3 −(3/4)z+((sin 3α)/4)=0 we know that sin 3α =3sin α −4sin^3 α ⇔ ⇔ sin^3 α −(3/4)sin α +((sin 3α)/4)=0 we can put z=sin α and get the solution
$$\left(\mathrm{1}\right)\:\:{x}^{\mathrm{3}} +{px}+{q}=\mathrm{0} \\ $$$${D}=\frac{{p}^{\mathrm{3}} }{\mathrm{27}}+\frac{{q}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\mathrm{if}\:{D}\geqslant\mathrm{0}\:\Rightarrow\:\mathrm{Cardano}'\mathrm{s}\:\mathrm{solution} \\ $$$$\mathrm{if}\:{D}<\mathrm{0}: \\ $$$$\frac{{p}^{\mathrm{3}} }{\mathrm{27}}+\frac{{q}^{\mathrm{2}} }{\mathrm{4}}<\mathrm{0}\:\Leftrightarrow\:−\mathrm{1}<\frac{\mathrm{27}{q}^{\mathrm{2}} }{\mathrm{4}{p}^{\mathrm{3}} }<\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{we}\:\mathrm{can}\:\mathrm{put}\:\frac{\mathrm{27}{q}^{\mathrm{2}} }{\mathrm{4}{p}^{\mathrm{3}} }=\mathrm{sin}\:\theta\:\mathrm{but}\:\mathrm{it}'\mathrm{s}\:\mathrm{convenient} \\ $$$$\mathrm{to}\:\mathrm{let}\:\theta=\mathrm{3}\alpha \\ $$$$\frac{\mathrm{27}{q}^{\mathrm{2}} }{\mathrm{4}{p}^{\mathrm{3}} }=\mathrm{sin}\:\mathrm{3}\alpha \\ $$$$\mathrm{now}\:\mathrm{let}\:{x}={az}\:\mathrm{and}\:{a}=\mathrm{2}\sqrt{\frac{−{p}}{\mathrm{3}}}\:\Rightarrow\:\mathrm{equation}\:\left(\mathrm{1}\right) \\ $$$$\mathrm{becomes} \\ $$$${a}^{\mathrm{3}} {z}^{\mathrm{3}} +{az}+{q}=\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\mathrm{4}{z}^{\mathrm{3}} −\mathrm{3}{z}−\frac{\mathrm{3}\sqrt{\mathrm{3}}{q}}{\:\mathrm{2}\sqrt{−{p}^{\mathrm{3}} }}=\mathrm{0} \\ $$$$\mathrm{now}\:\left(−\frac{\mathrm{3}\sqrt{\mathrm{3}}{q}}{\:\mathrm{2}\sqrt{−{p}^{\mathrm{3}} }}\right)^{\mathrm{2}} =\mid\frac{\mathrm{27}{q}^{\mathrm{2}} }{\mathrm{4}{p}^{\mathrm{3}} }\mid=\mathrm{sin}\:\mathrm{3}\alpha \\ $$$$\mathrm{4}{z}^{\mathrm{3}} −\mathrm{3}{z}+\mathrm{sin}\:\mathrm{3}\alpha\:=\mathrm{0} \\ $$$${z}^{\mathrm{3}} −\frac{\mathrm{3}}{\mathrm{4}}{z}+\frac{\mathrm{sin}\:\mathrm{3}\alpha}{\mathrm{4}}=\mathrm{0} \\ $$$$\mathrm{we}\:\mathrm{know}\:\mathrm{that}\:\mathrm{sin}\:\mathrm{3}\alpha\:=\mathrm{3sin}\:\alpha\:−\mathrm{4sin}^{\mathrm{3}} \:\alpha\:\Leftrightarrow \\ $$$$\Leftrightarrow\:\mathrm{sin}^{\mathrm{3}} \:\alpha\:−\frac{\mathrm{3}}{\mathrm{4}}\mathrm{sin}\:\alpha\:+\frac{\mathrm{sin}\:\mathrm{3}\alpha}{\mathrm{4}}=\mathrm{0} \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{put}\:{z}=\mathrm{sin}\:\alpha\:\mathrm{and}\:\mathrm{get}\:\mathrm{the}\:\mathrm{solution} \\ $$
Answered by Olaf last updated on 19/Sep/20
x = u+v 3(u^3 +v^3 )+9uv(u+v)−3(u+v)−(1/2) = 0 3(u^3 +v^3 )+3(u+v)(3uv−1)−(1/2) = 0 we choose u and v such as uv = (1/3) ⇒ u^3 v^3 = (1/(27)) and 3(u^3 +v^3 )−(1/2) = 0 u^3 +v^3 = (1/6) Let U = u^3 , V = v^3 and S = U+V = (1/6), P = UV = (1/(27)) We know S and P : z^2 −Sz+P = 0 Δ = S^2 −4P = (1/(36))−(4/(27)) = −((13)/(108)) U = ((S−(√Δ))/2) = (1/2)((1/6)−(1/6)i(√((13)/3))) U = ((S−(√Δ))/2) = (1/(12))(1−i(√((13)/3))) V = ((S+(√Δ))/2) = (1/(12))(1+i(√((13)/3))) ∣U∣ = ∣V∣ = (1/(12))×(√((16)/3)) = (1/(3(√3))) Let θ = ArgU = −ArgV = arctan(√((13)/3)) U = (1/(3(√3)))e^(iθ) and V = (1/(3(√3)))e^(−iθ) u = ^3 (√U) = (1/( (√3)))e^(i((θ/3)+((2kπ)/3))) k = 0,1,2 v = ^3 (√V) = (1/( (√3)))e^(i(−(θ/3)+((2kπ)/3))) k = 0,1,2 for k = 0, u = (1/( (√3)))e^(i(θ/3)) and v = (1/( (√3)))e^(−i(θ/3)) x = u+v = (1/( (√3)))(e^(i(θ/3)) +e^(−i(θ/3)) ) x = u+v = (2/( (√3)))cos(θ/3) x = u+v = (2/( (√3)))cos((1/3)arctan(√((13)/3))) we have the first root...
$$ \\ $$$${x}\:=\:{u}+{v} \\ $$$$\mathrm{3}\left({u}^{\mathrm{3}} +{v}^{\mathrm{3}} \right)+\mathrm{9}{uv}\left({u}+{v}\right)−\mathrm{3}\left({u}+{v}\right)−\frac{\mathrm{1}}{\mathrm{2}}\:=\:\mathrm{0} \\ $$$$\mathrm{3}\left({u}^{\mathrm{3}} +{v}^{\mathrm{3}} \right)+\mathrm{3}\left({u}+{v}\right)\left(\mathrm{3}{uv}−\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{2}}\:=\:\mathrm{0} \\ $$$$\mathrm{we}\:\mathrm{choose}\:{u}\:\mathrm{and}\:{v}\:\mathrm{such}\:\mathrm{as}\:{uv}\:=\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow\:{u}^{\mathrm{3}} {v}^{\mathrm{3}} \:=\:\frac{\mathrm{1}}{\mathrm{27}} \\ $$$$\mathrm{and}\:\mathrm{3}\left({u}^{\mathrm{3}} +{v}^{\mathrm{3}} \right)−\frac{\mathrm{1}}{\mathrm{2}}\:=\:\mathrm{0} \\ $$$${u}^{\mathrm{3}} +{v}^{\mathrm{3}} \:=\:\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$\mathrm{Let}\:\mathrm{U}\:=\:{u}^{\mathrm{3}} ,\:\mathrm{V}\:=\:{v}^{\mathrm{3}} \\ $$$$\mathrm{and}\:\mathrm{S}\:=\:\mathrm{U}+\mathrm{V}\:=\:\frac{\mathrm{1}}{\mathrm{6}},\:\mathrm{P}\:=\:\mathrm{UV}\:=\:\frac{\mathrm{1}}{\mathrm{27}} \\ $$$$\mathrm{We}\:\mathrm{know}\:\mathrm{S}\:\mathrm{and}\:\mathrm{P}\:: \\ $$$${z}^{\mathrm{2}} −\mathrm{S}{z}+\mathrm{P}\:=\:\mathrm{0} \\ $$$$\Delta\:=\:\mathrm{S}^{\mathrm{2}} −\mathrm{4P}\:=\:\frac{\mathrm{1}}{\mathrm{36}}−\frac{\mathrm{4}}{\mathrm{27}}\:=\:−\frac{\mathrm{13}}{\mathrm{108}} \\ $$$$\mathrm{U}\:=\:\frac{\mathrm{S}−\sqrt{\Delta}}{\mathrm{2}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{6}}−\frac{\mathrm{1}}{\mathrm{6}}{i}\sqrt{\frac{\mathrm{13}}{\mathrm{3}}}\right) \\ $$$$\mathrm{U}\:=\:\frac{\mathrm{S}−\sqrt{\Delta}}{\mathrm{2}}\:=\:\frac{\mathrm{1}}{\mathrm{12}}\left(\mathrm{1}−{i}\sqrt{\frac{\mathrm{13}}{\mathrm{3}}}\right) \\ $$$$\mathrm{V}\:=\:\frac{\mathrm{S}+\sqrt{\Delta}}{\mathrm{2}}\:=\:\frac{\mathrm{1}}{\mathrm{12}}\left(\mathrm{1}+{i}\sqrt{\frac{\mathrm{13}}{\mathrm{3}}}\right) \\ $$$$\mid\mathrm{U}\mid\:=\:\mid\mathrm{V}\mid\:=\:\frac{\mathrm{1}}{\mathrm{12}}×\sqrt{\frac{\mathrm{16}}{\mathrm{3}}}\:=\:\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$$$\mathrm{Let}\:\theta\:=\:\mathrm{ArgU}\:=\:−\mathrm{ArgV}\:=\:\mathrm{arctan}\sqrt{\frac{\mathrm{13}}{\mathrm{3}}} \\ $$$$\mathrm{U}\:=\:\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{3}}}{e}^{{i}\theta} \:\mathrm{and}\:\mathrm{V}\:=\:\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{3}}}{e}^{−{i}\theta} \\ $$$${u}\:=\overset{\mathrm{3}} {\:}\sqrt{\mathrm{U}}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}{e}^{{i}\left(\frac{\theta}{\mathrm{3}}+\frac{\mathrm{2}{k}\pi}{\mathrm{3}}\right)} \:{k}\:=\:\mathrm{0},\mathrm{1},\mathrm{2} \\ $$$${v}\:=\overset{\mathrm{3}} {\:}\sqrt{\mathrm{V}}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}{e}^{{i}\left(−\frac{\theta}{\mathrm{3}}+\frac{\mathrm{2}{k}\pi}{\mathrm{3}}\right)} \:{k}\:=\:\mathrm{0},\mathrm{1},\mathrm{2} \\ $$$$\mathrm{for}\:{k}\:=\:\mathrm{0},\:{u}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}{e}^{{i}\frac{\theta}{\mathrm{3}}} \:\mathrm{and}\:{v}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}{e}^{−{i}\frac{\theta}{\mathrm{3}}} \\ $$$${x}\:=\:{u}+{v}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\left({e}^{{i}\frac{\theta}{\mathrm{3}}} +{e}^{−{i}\frac{\theta}{\mathrm{3}}} \right) \\ $$$${x}\:=\:{u}+{v}\:=\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\mathrm{cos}\frac{\theta}{\mathrm{3}} \\ $$$${x}\:=\:{u}+{v}\:=\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\mathrm{cos}\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arctan}\sqrt{\frac{\mathrm{13}}{\mathrm{3}}}\right) \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{the}\:\mathrm{first}\:\mathrm{root}… \\ $$
Commented by MJS_new last updated on 19/Sep/20
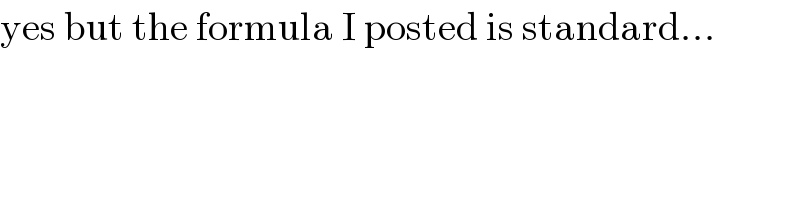
yes but the formula I posted is standard...
$$\mathrm{yes}\:\mathrm{but}\:\mathrm{the}\:\mathrm{formula}\:\mathrm{I}\:\mathrm{posted}\:\mathrm{is}\:\mathrm{standard}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *