Question Number 55310 by afachri last updated on 21/Feb/19
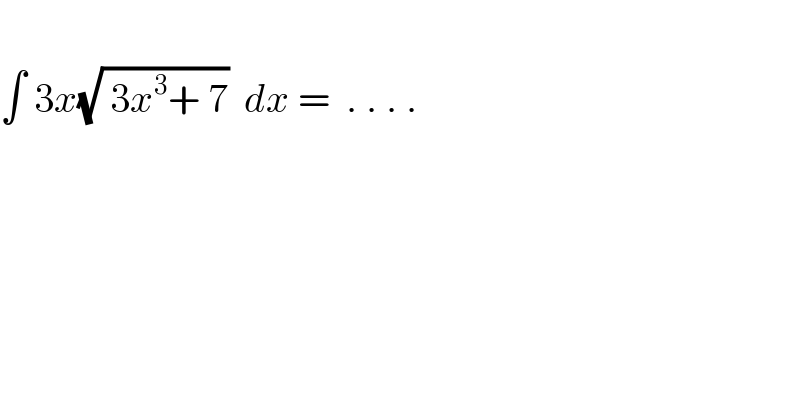
$$ \\ $$$$\int\:\mathrm{3}{x}\sqrt{\:\mathrm{3}{x}^{\mathrm{3}} +\:\mathrm{7}}\:\:{dx}\:=\:\:.\:.\:.\:. \\ $$
Commented by MJS last updated on 22/Feb/19
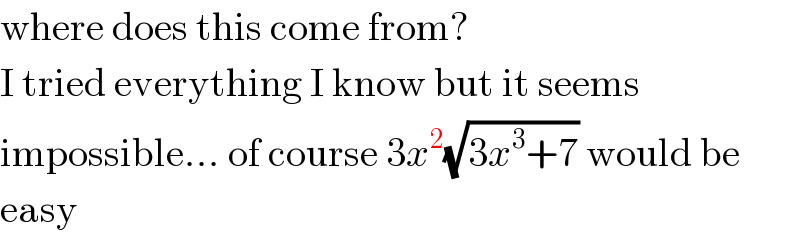
$$\mathrm{where}\:\mathrm{does}\:\mathrm{this}\:\mathrm{come}\:\mathrm{from}? \\ $$$$\mathrm{I}\:\mathrm{tried}\:\mathrm{everything}\:\mathrm{I}\:\mathrm{know}\:\mathrm{but}\:\mathrm{it}\:\mathrm{seems} \\ $$$$\mathrm{impossible}…\:\mathrm{of}\:\mathrm{course}\:\mathrm{3}{x}^{\mathrm{2}} \sqrt{\mathrm{3}{x}^{\mathrm{3}} +\mathrm{7}}\:\mathrm{would}\:\mathrm{be} \\ $$$$\mathrm{easy} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 21/Feb/19
![3x^3 =7tan^2 θ →x=(((7tan^2 θ)/3))^(1/3) 9x^2 dx=14tanθsec^2 θdθ dx=((14tanθsec^2 θdθ)/(9(((7tan^2 θ)/3))^(2/3) ))dθ ∫((3(((7tan^2 θ)/3))^(1/3) ×(√(7tan^2 θ +7)) ×14tanθsec^2 θdθ)/(9(((7tan^2 θ)/3))^(2/3) )) (3/9)∫(((√7) secθ×14tanθ×sec^2 θ)/(((7/3))^(2/3) ×(tanθ)^(4/3) ))dθ (1/3)×14(√7) ×((3/7))^(2/3) ∫((sec^3 θ)/((tanθ)^(1/3) ))dθ I=∫((sec^3 θ)/((tanθ)^(1/3) ))dθ secθ∫sec^2 θ×(1/((tanθ)^(1/3) ))dθ−∫[(d/dθ)(secθ)∫((sec^2 θ)/((tanθ)^(1/3) ))dθ]dθ secθ×(((tanθ)^(((−1)/3)+1) )/(2/3))−∫secθtanθ×(((tanθ)^(2/3) )/(2/3))dθ (3/2)secθ(tanθ)^(2/3) −(3/2)∫secθtanθ(sec^2 θ−1)^(1/3) dθ (3/2)secθ(tanθ)^(3/2) −(3/2)∫(a^2 −1)^(1/3) da curfew in headquater...that is brain...wait...](https://www.tinkutara.com/question/Q55313.png)
$$\mathrm{3}{x}^{\mathrm{3}} =\mathrm{7}{tan}^{\mathrm{2}} \theta\:\rightarrow{x}=\left(\frac{\mathrm{7}{tan}^{\mathrm{2}} \theta}{\mathrm{3}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$\mathrm{9}{x}^{\mathrm{2}} {dx}=\mathrm{14}{tan}\theta{sec}^{\mathrm{2}} \theta{d}\theta \\ $$$${dx}=\frac{\mathrm{14}{tan}\theta{sec}^{\mathrm{2}} \theta{d}\theta}{\mathrm{9}\left(\frac{\mathrm{7}{tan}^{\mathrm{2}} \theta}{\mathrm{3}}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} }{d}\theta \\ $$$$\int\frac{\mathrm{3}\left(\frac{\mathrm{7}{tan}^{\mathrm{2}} \theta}{\mathrm{3}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} ×\sqrt{\mathrm{7}{tan}^{\mathrm{2}} \theta\:+\mathrm{7}}\:×\mathrm{14}{tan}\theta{sec}^{\mathrm{2}} \theta{d}\theta}{\mathrm{9}\left(\frac{\mathrm{7}{tan}^{\mathrm{2}} \theta}{\mathrm{3}}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} } \\ $$$$\frac{\mathrm{3}}{\mathrm{9}}\int\frac{\sqrt{\mathrm{7}}\:{sec}\theta×\mathrm{14}{tan}\theta×{sec}^{\mathrm{2}} \theta}{\left(\frac{\mathrm{7}}{\mathrm{3}}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} ×\left({tan}\theta\right)^{\frac{\mathrm{4}}{\mathrm{3}}} }{d}\theta \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}×\mathrm{14}\sqrt{\mathrm{7}}\:×\left(\frac{\mathrm{3}}{\mathrm{7}}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} \int\frac{{sec}^{\mathrm{3}} \theta}{\left({tan}\theta\right)^{\frac{\mathrm{1}}{\mathrm{3}}} }{d}\theta \\ $$$$ \\ $$$${I}=\int\frac{{sec}^{\mathrm{3}} \theta}{\left({tan}\theta\right)^{\frac{\mathrm{1}}{\mathrm{3}}} }{d}\theta \\ $$$${sec}\theta\int{sec}^{\mathrm{2}} \theta×\frac{\mathrm{1}}{\left({tan}\theta\right)^{\frac{\mathrm{1}}{\mathrm{3}}} }{d}\theta−\int\left[\frac{{d}}{{d}\theta}\left({sec}\theta\right)\int\frac{{sec}^{\mathrm{2}} \theta}{\left({tan}\theta\right)^{\frac{\mathrm{1}}{\mathrm{3}}} }{d}\theta\right]{d}\theta \\ $$$${sec}\theta×\frac{\left({tan}\theta\right)^{\frac{−\mathrm{1}}{\mathrm{3}}+\mathrm{1}} }{\frac{\mathrm{2}}{\mathrm{3}}}−\int{sec}\theta{tan}\theta×\frac{\left({tan}\theta\right)^{\frac{\mathrm{2}}{\mathrm{3}}} }{\frac{\mathrm{2}}{\mathrm{3}}}{d}\theta \\ $$$$\frac{\mathrm{3}}{\mathrm{2}}{sec}\theta\left({tan}\theta\right)^{\frac{\mathrm{2}}{\mathrm{3}}} \:−\frac{\mathrm{3}}{\mathrm{2}}\int{sec}\theta{tan}\theta\left({sec}^{\mathrm{2}} \theta−\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} {d}\theta \\ $$$$\frac{\mathrm{3}}{\mathrm{2}}{sec}\theta\left({tan}\theta\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\frac{\mathrm{3}}{\mathrm{2}}\int\left({a}^{\mathrm{2}} −\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} {da} \\ $$$${curfew}\:{in}\:{headquater}…{that}\:{is}\:{brain}…{wait}… \\ $$$$ \\ $$$$ \\ $$
Commented by afachri last updated on 21/Feb/19
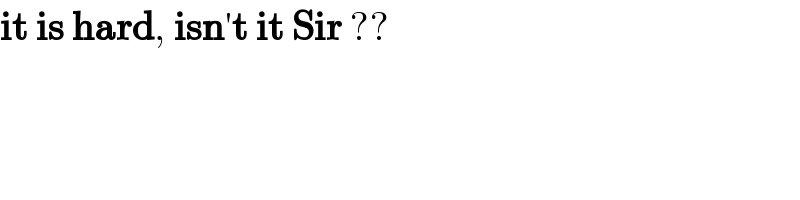
$$\boldsymbol{\mathrm{it}}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{hard}},\:\boldsymbol{\mathrm{isn}}'\boldsymbol{\mathrm{t}}\:\boldsymbol{\mathrm{it}}\:\boldsymbol{\mathrm{Sir}}\:?? \\ $$
Commented by afachri last updated on 21/Feb/19

$$\boldsymbol{\mathrm{oh}}\:\boldsymbol{\mathrm{sir}},\:\boldsymbol{\mathrm{i}}\:\boldsymbol{\mathrm{think}}\:\boldsymbol{\mathrm{my}}\:\boldsymbol{\mathrm{mind}}\:\boldsymbol{\mathrm{has}}\:\boldsymbol{\mathrm{blown}}. \\ $$$$\boldsymbol{\mathrm{hehehe}}… \\ $$
