Question Number 29222 by imamu222 last updated on 05/Feb/18
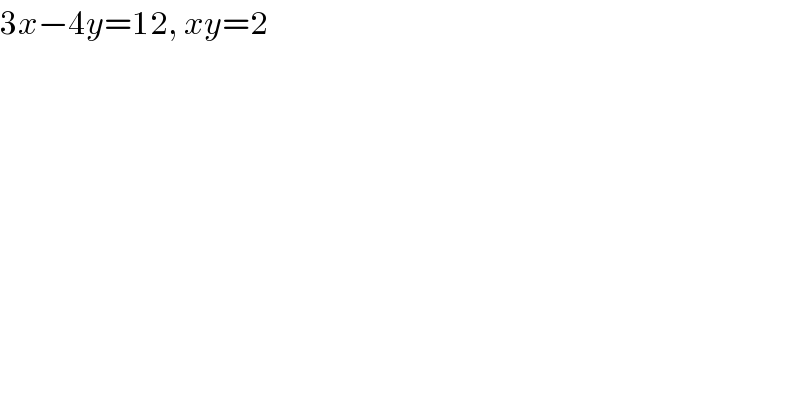
$$\mathrm{3}{x}−\mathrm{4}{y}=\mathrm{12},\:{xy}=\mathrm{2} \\ $$
Answered by ajfour last updated on 05/Feb/18
![3x−(8/x)=12 3x^2 −12x=8 3(x^2 −4x)=8 3(x−2)^2 =20 x=2±2(√(5/3)) y=(1/(1±(√(5/3)))) =((1∓(√(5/3)))/(−(2/3))) (x_1 ,y_1 )≡ [2(1+(√(5/3)) ), (3/2)((√(5/3))−1)] (x_2 ,y_2 )≡ [2(1−(√(5/3)) ),−(3/2)((√(5/3))+1)] .](https://www.tinkutara.com/question/Q29224.png)
$$\mathrm{3}{x}−\frac{\mathrm{8}}{{x}}=\mathrm{12} \\ $$$$\mathrm{3}{x}^{\mathrm{2}} −\mathrm{12}{x}=\mathrm{8} \\ $$$$\mathrm{3}\left({x}^{\mathrm{2}} −\mathrm{4}{x}\right)=\mathrm{8} \\ $$$$\mathrm{3}\left({x}−\mathrm{2}\right)^{\mathrm{2}} =\mathrm{20} \\ $$$${x}=\mathrm{2}\pm\mathrm{2}\sqrt{\frac{\mathrm{5}}{\mathrm{3}}}\:\: \\ $$$${y}=\frac{\mathrm{1}}{\mathrm{1}\pm\sqrt{\frac{\mathrm{5}}{\mathrm{3}}}}\:=\frac{\mathrm{1}\mp\sqrt{\frac{\mathrm{5}}{\mathrm{3}}}}{−\frac{\mathrm{2}}{\mathrm{3}}} \\ $$$$\left({x}_{\mathrm{1}} ,{y}_{\mathrm{1}} \right)\equiv\:\left[\mathrm{2}\left(\mathrm{1}+\sqrt{\frac{\mathrm{5}}{\mathrm{3}}}\:\right),\:\frac{\mathrm{3}}{\mathrm{2}}\left(\sqrt{\frac{\mathrm{5}}{\mathrm{3}}}−\mathrm{1}\right)\right] \\ $$$$\left({x}_{\mathrm{2}} ,{y}_{\mathrm{2}} \right)\equiv\:\left[\mathrm{2}\left(\mathrm{1}−\sqrt{\frac{\mathrm{5}}{\mathrm{3}}}\:\right),−\frac{\mathrm{3}}{\mathrm{2}}\left(\sqrt{\frac{\mathrm{5}}{\mathrm{3}}}+\mathrm{1}\right)\right]\:. \\ $$
