Menu Close

3x-5-x-4-9x-3-12x-2-2x-1-x-3-1-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 101985 by I want to learn more last updated on 06/Jul/20
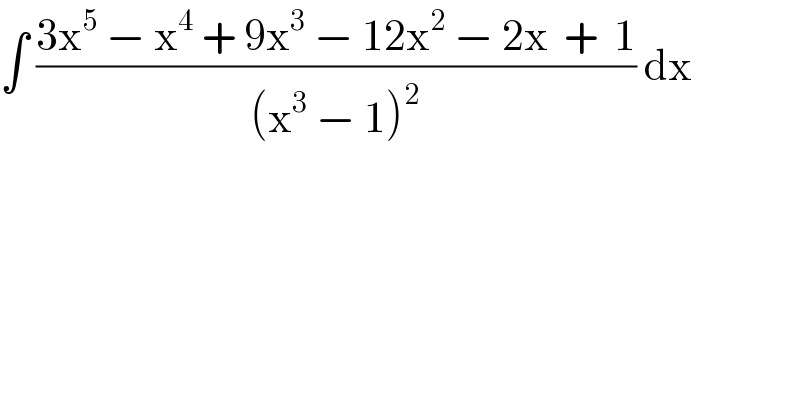
∫ ((3x^5 − x^4 + 9x^3 − 12x^2 − 2x + 1)/((x^3 − 1)^2 )) dx
$$\int\:\frac{\mathrm{3x}^{\mathrm{5}} \:−\:\mathrm{x}^{\mathrm{4}} \:+\:\mathrm{9x}^{\mathrm{3}} \:−\:\mathrm{12x}^{\mathrm{2}} \:−\:\mathrm{2x}\:\:+\:\:\mathrm{1}}{\left(\mathrm{x}^{\mathrm{3}} \:−\:\mathrm{1}\right)^{\mathrm{2}} }\:\mathrm{dx} \\ $$
Answered by 1549442205 last updated on 06/Jul/20
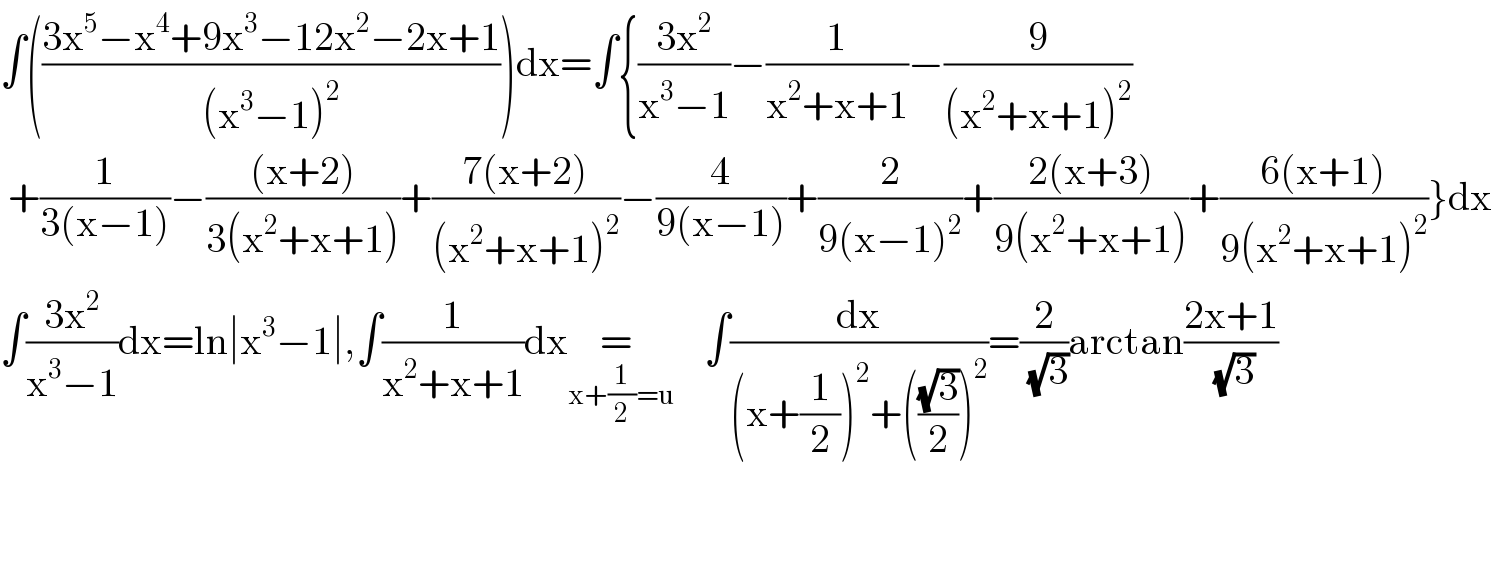
∫(((3x^5 −x^4 +9x^3 −12x^2 −2x+1)/((x^3 −1)^2 )))dx=∫{((3x^2 )/(x^3 −1))−(1/(x^2 +x+1))−(9/((x^2 +x+1)^2 )) +(1/(3(x−1)))−(((x+2))/(3(x^2 +x+1)))+((7(x+2))/((x^2 +x+1)^2 ))−(4/(9(x−1)))+(2/(9(x−1)^2 ))+((2(x+3))/(9(x^2 +x+1)))+((6(x+1))/(9(x^2 +x+1)^2 ))}dx ∫((3x^2 )/(x^3 −1))dx=ln∣x^3 −1∣,∫(1/(x^2 +x+1))dx= _(x+(1/2)=u) ∫(dx/((x+(1/2))^2 +(((√3)/2))^2 ))=(2/( (√3)))arctan((2x+1)/( (√3)))
$$\int\left(\frac{\mathrm{3x}^{\mathrm{5}} −\mathrm{x}^{\mathrm{4}} +\mathrm{9x}^{\mathrm{3}} −\mathrm{12x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{1}}{\left(\mathrm{x}^{\mathrm{3}} −\mathrm{1}\right)^{\mathrm{2}} }\right)\mathrm{dx}=\int\left\{\frac{\mathrm{3x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{3}} −\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}−\frac{\mathrm{9}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\right. \\ $$$$\left.\:+\frac{\mathrm{1}}{\mathrm{3}\left(\mathrm{x}−\mathrm{1}\right)}−\frac{\left(\mathrm{x}+\mathrm{2}\right)}{\mathrm{3}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)}+\frac{\mathrm{7}\left(\mathrm{x}+\mathrm{2}\right)}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{4}}{\mathrm{9}\left(\mathrm{x}−\mathrm{1}\right)}+\frac{\mathrm{2}}{\mathrm{9}\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{2}\left(\mathrm{x}+\mathrm{3}\right)}{\mathrm{9}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)}+\frac{\mathrm{6}\left(\mathrm{x}+\mathrm{1}\right)}{\mathrm{9}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\right\}\mathrm{dx} \\ $$$$\int\frac{\mathrm{3x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{3}} −\mathrm{1}}\mathrm{dx}=\mathrm{ln}\mid\mathrm{x}^{\mathrm{3}} −\mathrm{1}\mid,\int\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\mathrm{dx}\underset{\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{u}} {=\:}\:\:\:\:\int\frac{\mathrm{dx}}{\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\mathrm{arctan}\frac{\mathrm{2x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$$ \\ $$$$ \\ $$
Commented by I want to learn more last updated on 07/Jul/20
Thanks sir.
$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *