Question Number 83159 by jagoll last updated on 28/Feb/20
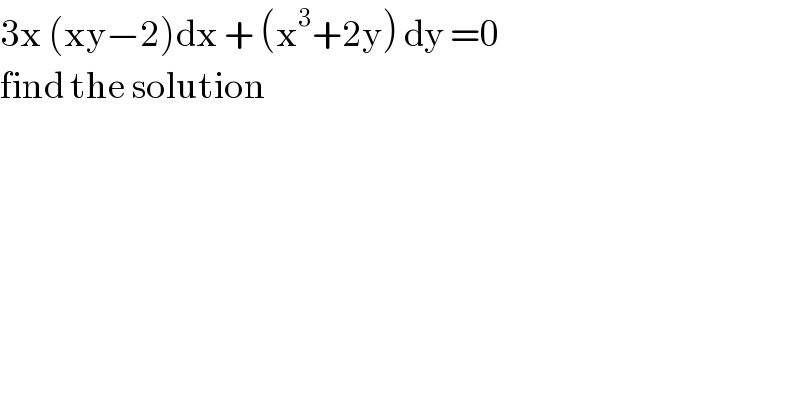
$$\mathrm{3x}\:\left(\mathrm{xy}−\mathrm{2}\right)\mathrm{dx}\:+\:\left(\mathrm{x}^{\mathrm{3}} +\mathrm{2y}\right)\:\mathrm{dy}\:=\mathrm{0} \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{solution} \\ $$
Commented by niroj last updated on 28/Feb/20
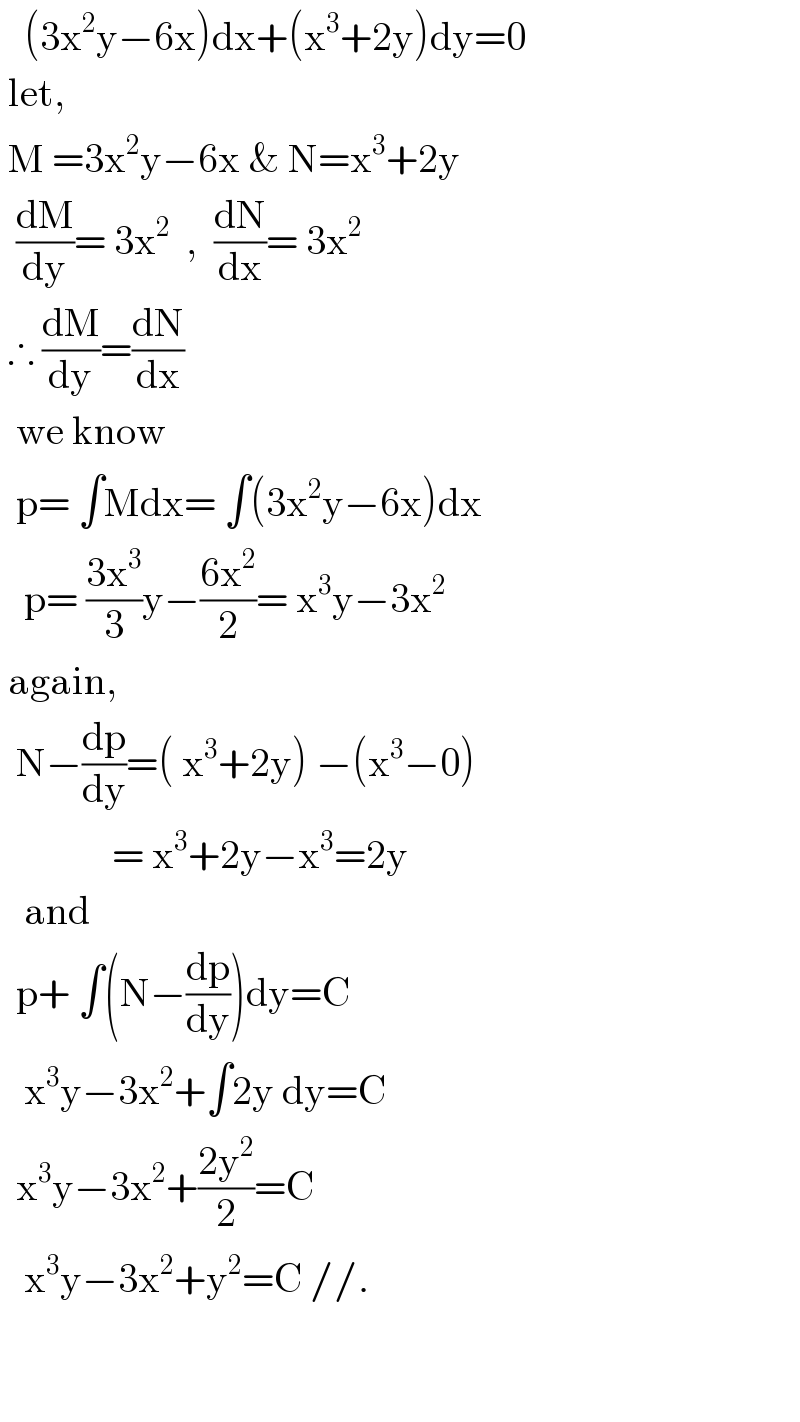
$$\:\:\:\left(\mathrm{3x}^{\mathrm{2}} \mathrm{y}−\mathrm{6x}\right)\mathrm{dx}+\left(\mathrm{x}^{\mathrm{3}} +\mathrm{2y}\right)\mathrm{dy}=\mathrm{0} \\ $$$$\:\mathrm{let},\: \\ $$$$\:\mathrm{M}\:=\mathrm{3x}^{\mathrm{2}} \mathrm{y}−\mathrm{6x}\:\&\:\mathrm{N}=\mathrm{x}^{\mathrm{3}} +\mathrm{2y} \\ $$$$\:\:\frac{\mathrm{dM}}{\mathrm{dy}}=\:\mathrm{3x}^{\mathrm{2}} \:\:,\:\:\frac{\mathrm{dN}}{\mathrm{dx}}=\:\mathrm{3x}^{\mathrm{2}} \\ $$$$\:\therefore\:\frac{\mathrm{dM}}{\mathrm{dy}}=\frac{\mathrm{dN}}{\mathrm{dx}} \\ $$$$\:\:\mathrm{we}\:\mathrm{know} \\ $$$$\:\:\mathrm{p}=\:\int\mathrm{Mdx}=\:\int\left(\mathrm{3x}^{\mathrm{2}} \mathrm{y}−\mathrm{6x}\right)\mathrm{dx} \\ $$$$\:\:\:\mathrm{p}=\:\frac{\mathrm{3x}^{\mathrm{3}} }{\mathrm{3}}\mathrm{y}−\frac{\mathrm{6x}^{\mathrm{2}} }{\mathrm{2}}=\:\mathrm{x}^{\mathrm{3}} \mathrm{y}−\mathrm{3x}^{\mathrm{2}} \\ $$$$\:\mathrm{again}, \\ $$$$\:\:\mathrm{N}−\frac{\mathrm{dp}}{\mathrm{dy}}=\left(\:\mathrm{x}^{\mathrm{3}} +\mathrm{2y}\right)\:−\left(\mathrm{x}^{\mathrm{3}} −\mathrm{0}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{x}^{\mathrm{3}} +\mathrm{2y}−\mathrm{x}^{\mathrm{3}} =\mathrm{2y} \\ $$$$\:\:\:\mathrm{and} \\ $$$$\:\:\mathrm{p}+\:\int\left(\mathrm{N}−\frac{\mathrm{dp}}{\mathrm{dy}}\right)\mathrm{dy}=\mathrm{C} \\ $$$$\:\:\:\mathrm{x}^{\mathrm{3}} \mathrm{y}−\mathrm{3x}^{\mathrm{2}} +\int\mathrm{2y}\:\mathrm{dy}=\mathrm{C} \\ $$$$\:\:\mathrm{x}^{\mathrm{3}} \mathrm{y}−\mathrm{3x}^{\mathrm{2}} +\frac{\mathrm{2y}^{\mathrm{2}} }{\mathrm{2}}=\mathrm{C} \\ $$$$\:\:\:\mathrm{x}^{\mathrm{3}} \mathrm{y}−\mathrm{3x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} =\mathrm{C}\://. \\ $$$$\:\: \\ $$$$\:\: \\ $$
Commented by jagoll last updated on 28/Feb/20
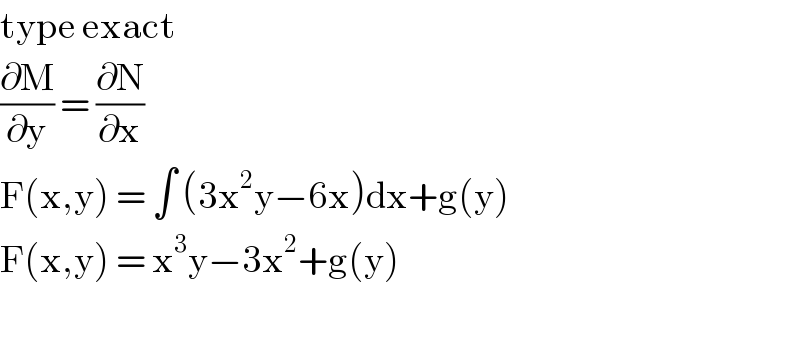
$$\mathrm{type}\:\mathrm{exact} \\ $$$$\frac{\partial\mathrm{M}}{\partial\mathrm{y}}\:=\:\frac{\partial\mathrm{N}}{\partial\mathrm{x}} \\ $$$$\mathrm{F}\left(\mathrm{x},\mathrm{y}\right)\:=\:\int\:\left(\mathrm{3x}^{\mathrm{2}} \mathrm{y}−\mathrm{6x}\right)\mathrm{dx}+\mathrm{g}\left(\mathrm{y}\right) \\ $$$$\mathrm{F}\left(\mathrm{x},\mathrm{y}\right)\:=\:\mathrm{x}^{\mathrm{3}} \mathrm{y}−\mathrm{3x}^{\mathrm{2}} +\mathrm{g}\left(\mathrm{y}\right) \\ $$$$ \\ $$
Commented by jagoll last updated on 28/Feb/20
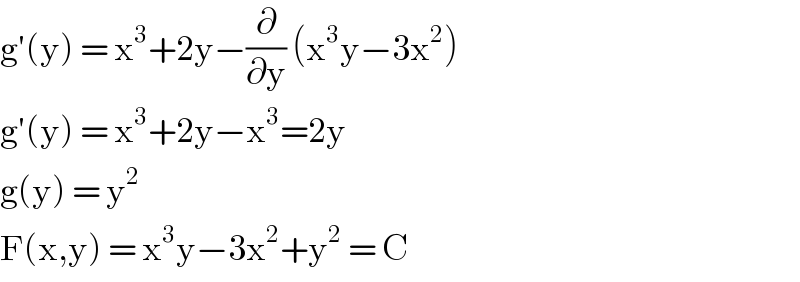
$$\mathrm{g}'\left(\mathrm{y}\right)\:=\:\mathrm{x}^{\mathrm{3}} +\mathrm{2y}−\frac{\partial}{\partial\mathrm{y}}\:\left(\mathrm{x}^{\mathrm{3}} \mathrm{y}−\mathrm{3x}^{\mathrm{2}} \right) \\ $$$$\mathrm{g}'\left(\mathrm{y}\right)\:=\:\mathrm{x}^{\mathrm{3}} +\mathrm{2y}−\mathrm{x}^{\mathrm{3}} =\mathrm{2y} \\ $$$$\mathrm{g}\left(\mathrm{y}\right)\:=\:\mathrm{y}^{\mathrm{2}} \\ $$$$\mathrm{F}\left(\mathrm{x},\mathrm{y}\right)\:=\:\mathrm{x}^{\mathrm{3}} \mathrm{y}−\mathrm{3x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \:=\:\mathrm{C} \\ $$
Commented by peter frank last updated on 28/Feb/20
$${thank}\:{you}\:{both} \\ $$
Commented by niroj last updated on 28/Feb/20
$$\mathrm{you}\:\mathrm{must}\:\mathrm{welcome}\:\mathrm{dear}. \\ $$
Answered by TANMAY PANACEA last updated on 28/Feb/20
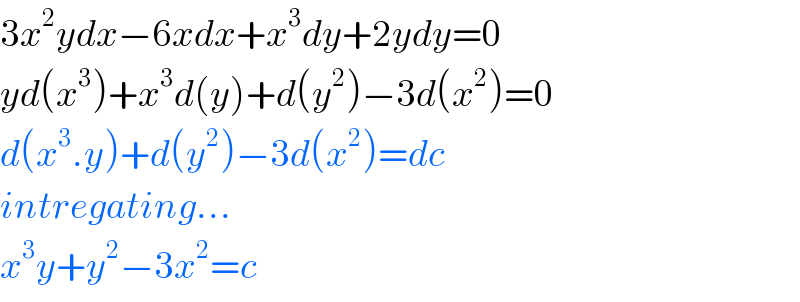
$$\mathrm{3}{x}^{\mathrm{2}} {ydx}−\mathrm{6}{xdx}+{x}^{\mathrm{3}} {dy}+\mathrm{2}{ydy}=\mathrm{0} \\ $$$${yd}\left({x}^{\mathrm{3}} \right)+{x}^{\mathrm{3}} {d}\left({y}\right)+{d}\left({y}^{\mathrm{2}} \right)−\mathrm{3}{d}\left({x}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$${d}\left({x}^{\mathrm{3}} .{y}\right)+{d}\left({y}^{\mathrm{2}} \right)−\mathrm{3}{d}\left({x}^{\mathrm{2}} \right)={dc} \\ $$$${intregating}… \\ $$$${x}^{\mathrm{3}} {y}+{y}^{\mathrm{2}} −\mathrm{3}{x}^{\mathrm{2}} ={c} \\ $$
