Menu Close

3x-y-1-dx-6x-2y-3-dy-0-

Tinku Tara 0 Comments
Pin




Question Number 119290 by bobhans last updated on 23/Oct/20
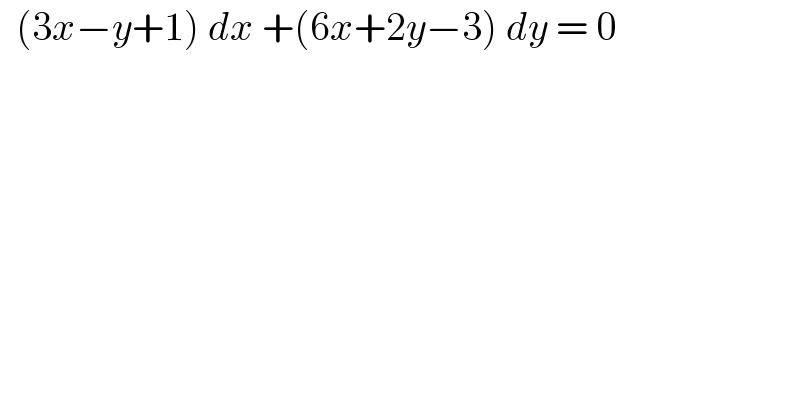
(3x−y+1) dx +(6x+2y−3) dy = 0
$$\:\:\left(\mathrm{3}{x}−{y}+\mathrm{1}\right)\:{dx}\:+\left(\mathrm{6}{x}+\mathrm{2}{y}−\mathrm{3}\right)\:{dy}\:=\:\mathrm{0}\: \\ $$
Answered by TANMAY PANACEA last updated on 23/Oct/20
dy(6x+2y−3)=(−3x+y−1)dx (dy/dx)=((−3x+y−1)/(6x+2y−3)) x=X+h y=Y+k (dY/dX)=((−3(X+h)+(Y+k)−1)/(6(X+h)+2(Y+k)−3)) (dY/dX)=((−3X+Y)/(6X+2Y)) note −3h+k−1=0 and 6h+2k−3=0 −3h+k−1=0 ×2 −6h+2k−2=0 6h+2k−3=0 so 4k=5→k=(5/4) 12h−1=0→h=(1/(12)) (dY/dX)=((−3X+Y)/(6X+2Y))=((−3+(Y/X))/(6+((2Y)/X)))→(homogeneous function) (Y/X)=v→(dY/dX)=v+X(dv/dX) v+X(dv/dX)=((−3+v)/(6+2v)) X(dv/dX)=((−3+v−6v−2v^2 )/(6+2v)) ((6+2v)/(−2v^2 −5v−3))dv=(dX/X) ((6+2v)/(2v^2 +5v+3))+(dX/X)=dC (1/2)∫((4v+5+7)/(2v^2 +5v+3))dv+∫(dX/X)=∫dC (1/2)∫((d(2v^2 +5v+3))/(2v^2 +5v+3))+(7/4)∫(dv/(v^2 +((5v)/2)+(3/2)))+∫(dX/X)=∫dC (1/2)∫((d(2v^2 +5v+3))/(2v^2 +5v+3))+(7/4)∫(dv/(v^2 +2×v×(5/4)+((25)/(16))+(3/2)−((25)/(16))))+∫(dX/X)=∫dC (1/2)∫((d(2v^2 +5v+3))/(2v^2 +5v+3))+(7/4)∫(dv/((v+(5/4))^2 −((1/4))^2 ))+∫(dX/X)=∫dC (1/2)ln(2v^2 +5v+3)+(7/4)∫pls use formula+lnX=C now v=(Y/X)=((y−k)/(X−h))=((y−(5/4))/(x−(1/(12))))
$${dy}\left(\mathrm{6}{x}+\mathrm{2}{y}−\mathrm{3}\right)=\left(−\mathrm{3}{x}+{y}−\mathrm{1}\right){dx} \\ $$$$\frac{{dy}}{{dx}}=\frac{−\mathrm{3}{x}+{y}−\mathrm{1}}{\mathrm{6}{x}+\mathrm{2}{y}−\mathrm{3}} \\ $$$${x}={X}+{h} \\ $$$${y}={Y}+{k} \\ $$$$\frac{{dY}}{{dX}}=\frac{−\mathrm{3}\left({X}+{h}\right)+\left({Y}+{k}\right)−\mathrm{1}}{\mathrm{6}\left({X}+{h}\right)+\mathrm{2}\left({Y}+{k}\right)−\mathrm{3}} \\ $$$$\frac{{dY}}{{dX}}=\frac{−\mathrm{3}{X}+{Y}}{\mathrm{6}{X}+\mathrm{2}{Y}} \\ $$$${note}\:\:−\mathrm{3}{h}+{k}−\mathrm{1}=\mathrm{0} \\ $$$${and}\:\:\mathrm{6}{h}+\mathrm{2}{k}−\mathrm{3}=\mathrm{0} \\ $$$$−\mathrm{3}{h}+{k}−\mathrm{1}=\mathrm{0}\:×\mathrm{2} \\ $$$$−\mathrm{6}{h}+\mathrm{2}{k}−\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{6}{h}+\mathrm{2}{k}−\mathrm{3}=\mathrm{0} \\ $$$${so}\:\mathrm{4}{k}=\mathrm{5}\rightarrow{k}=\frac{\mathrm{5}}{\mathrm{4}} \\ $$$$\mathrm{12}{h}−\mathrm{1}=\mathrm{0}\rightarrow{h}=\frac{\mathrm{1}}{\mathrm{12}} \\ $$$$\frac{{dY}}{{dX}}=\frac{−\mathrm{3}{X}+{Y}}{\mathrm{6}{X}+\mathrm{2}{Y}}=\frac{−\mathrm{3}+\frac{{Y}}{{X}}}{\mathrm{6}+\frac{\mathrm{2}{Y}}{{X}}}\rightarrow\left({homogeneous}\:{function}\right) \\ $$$$\frac{{Y}}{{X}}={v}\rightarrow\frac{{dY}}{{dX}}={v}+{X}\frac{{dv}}{{dX}} \\ $$$${v}+{X}\frac{{dv}}{{dX}}=\frac{−\mathrm{3}+{v}}{\mathrm{6}+\mathrm{2}{v}} \\ $$$${X}\frac{{dv}}{{dX}}=\frac{−\mathrm{3}+{v}−\mathrm{6}{v}−\mathrm{2}{v}^{\mathrm{2}} }{\mathrm{6}+\mathrm{2}{v}} \\ $$$$\frac{\mathrm{6}+\mathrm{2}{v}}{−\mathrm{2}{v}^{\mathrm{2}} −\mathrm{5}{v}−\mathrm{3}}{dv}=\frac{{dX}}{{X}} \\ $$$$\frac{\mathrm{6}+\mathrm{2}{v}}{\mathrm{2}{v}^{\mathrm{2}} +\mathrm{5}{v}+\mathrm{3}}+\frac{{dX}}{{X}}={dC} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{4}{v}+\mathrm{5}+\mathrm{7}}{\mathrm{2}{v}^{\mathrm{2}} +\mathrm{5}{v}+\mathrm{3}}{dv}+\int\frac{{dX}}{{X}}=\int{dC} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left(\mathrm{2}{v}^{\mathrm{2}} +\mathrm{5}{v}+\mathrm{3}\right)}{\mathrm{2}{v}^{\mathrm{2}} +\mathrm{5}{v}+\mathrm{3}}+\frac{\mathrm{7}}{\mathrm{4}}\int\frac{{dv}}{{v}^{\mathrm{2}} +\frac{\mathrm{5}{v}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{2}}}+\int\frac{{dX}}{{X}}=\int{dC} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left(\mathrm{2}{v}^{\mathrm{2}} +\mathrm{5}{v}+\mathrm{3}\right)}{\mathrm{2}{v}^{\mathrm{2}} +\mathrm{5}{v}+\mathrm{3}}+\frac{\mathrm{7}}{\mathrm{4}}\int\frac{{dv}}{{v}^{\mathrm{2}} +\mathrm{2}×{v}×\frac{\mathrm{5}}{\mathrm{4}}+\frac{\mathrm{25}}{\mathrm{16}}+\frac{\mathrm{3}}{\mathrm{2}}−\frac{\mathrm{25}}{\mathrm{16}}}+\int\frac{{dX}}{{X}}=\int{dC} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left(\mathrm{2}{v}^{\mathrm{2}} +\mathrm{5}{v}+\mathrm{3}\right)}{\mathrm{2}{v}^{\mathrm{2}} +\mathrm{5}{v}+\mathrm{3}}+\frac{\mathrm{7}}{\mathrm{4}}\int\frac{{dv}}{\left({v}+\frac{\mathrm{5}}{\mathrm{4}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} }+\int\frac{{dX}}{{X}}=\int{dC} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{2}{v}^{\mathrm{2}} +\mathrm{5}{v}+\mathrm{3}\right)+\frac{\mathrm{7}}{\mathrm{4}}\int{pls}\:{use}\:{formula}+{lnX}={C} \\ $$$${now}\:\:{v}=\frac{{Y}}{{X}}=\frac{{y}−{k}}{{X}−{h}}=\frac{{y}−\frac{\mathrm{5}}{\mathrm{4}}}{{x}−\frac{\mathrm{1}}{\mathrm{12}}} \\ $$
Commented by Dwaipayan Shikari last updated on 23/Oct/20
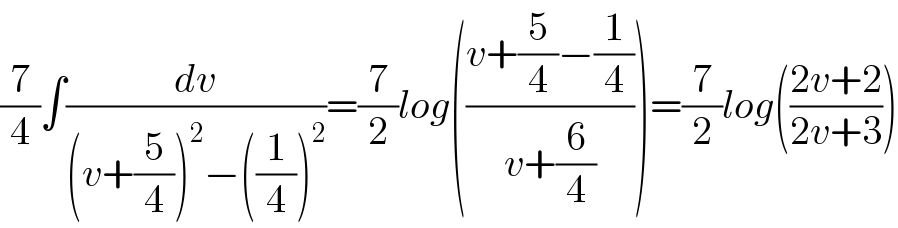
(7/4)∫(dv/((v+(5/4))^2 −((1/4))^2 ))=(7/2)log(((v+(5/4)−(1/4))/(v+(6/4))))=(7/2)log(((2v+2)/(2v+3)))
$$\frac{\mathrm{7}}{\mathrm{4}}\int\frac{{dv}}{\left({v}+\frac{\mathrm{5}}{\mathrm{4}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} }=\frac{\mathrm{7}}{\mathrm{2}}{log}\left(\frac{{v}+\frac{\mathrm{5}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{4}}}{{v}+\frac{\mathrm{6}}{\mathrm{4}}}\right)=\frac{\mathrm{7}}{\mathrm{2}}{log}\left(\frac{\mathrm{2}{v}+\mathrm{2}}{\mathrm{2}{v}+\mathrm{3}}\right) \\ $$
Commented by TANMAY PANACEA last updated on 23/Oct/20
thank you
$${thank}\:{you} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *