3xy-2-x-3-9-1-3x-2-y-y-3-18-2-Find-x-and-y-

Question Number 61744 by Cheyboy last updated on 08/Jun/19

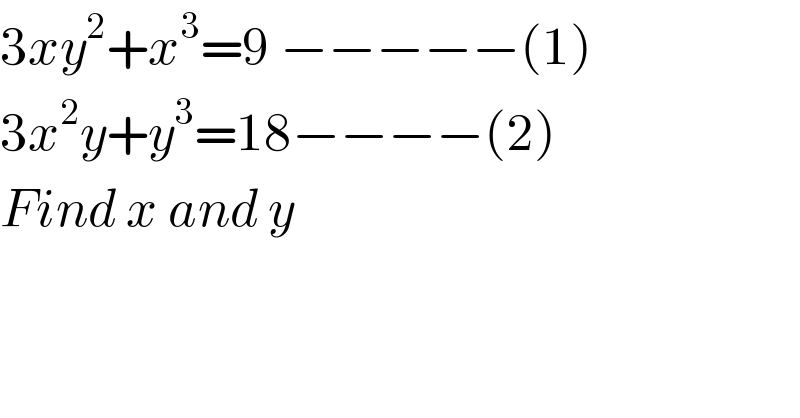
$$\mathrm{3}{xy}^{\mathrm{2}} +{x}^{\mathrm{3}} =\mathrm{9}\:−−−−−\left(\mathrm{1}\right) \\ $$$$\mathrm{3}{x}^{\mathrm{2}} {y}+{y}^{\mathrm{3}} =\mathrm{18}−−−−\left(\mathrm{2}\right) \\ $$$${Find}\:{x}\:{and}\:{y} \\ $$

Commented by Cheyboy last updated on 08/Jun/19

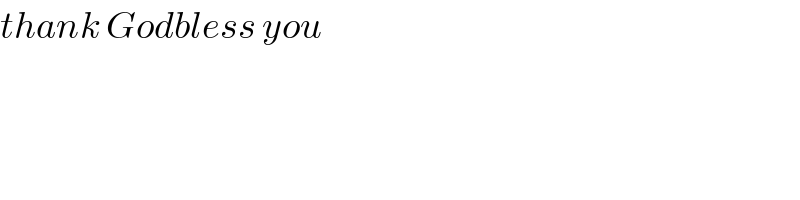
$${thank}\:{Godbless}\:{you} \\ $$

Commented by Cheyboy last updated on 08/Jun/19

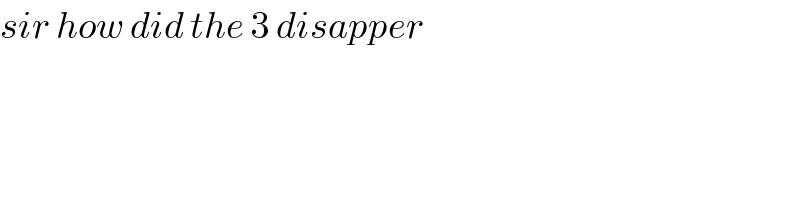
$${sir}\:{how}\:{did}\:{the}\:\mathrm{3}\:{disapper} \\ $$

Commented by Prithwish sen last updated on 08/Jun/19

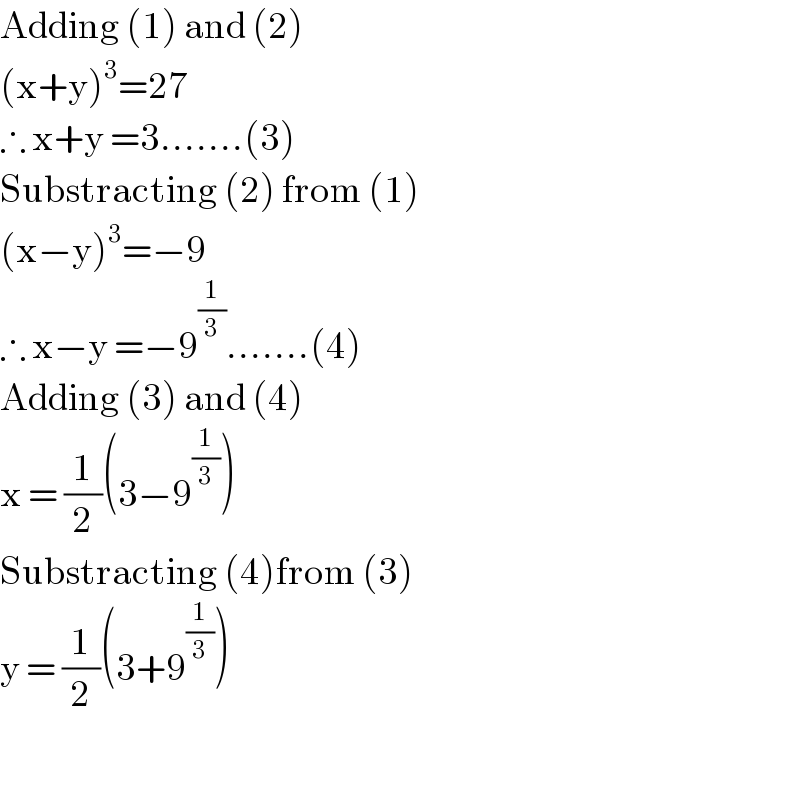
Adding (1) and (2) (x+y)^3 =27 ∴ x+y =3.......(3) Substracting (2) from (1) (x−y)^3 =−9 ∴ x−y =−9^(1/3) .......(4) Adding (3) and (4) x = (1/2)(3−9^(1/3) ) Substracting (4)from (3) y = (1/2)(3+9^(1/3) )

$$\mathrm{Adding}\:\left(\mathrm{1}\right)\:\mathrm{and}\:\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{3}} =\mathrm{27} \\ $$$$\therefore\:\mathrm{x}+\mathrm{y}\:=\mathrm{3}…….\left(\mathrm{3}\right) \\ $$$$\mathrm{Substracting}\:\left(\mathrm{2}\right)\:\mathrm{from}\:\left(\mathrm{1}\right) \\ $$$$\left(\mathrm{x}−\mathrm{y}\right)^{\mathrm{3}} =−\mathrm{9} \\ $$$$\therefore\:\mathrm{x}−\mathrm{y}\:=−\mathrm{9}^{\frac{\mathrm{1}}{\mathrm{3}}} …….\left(\mathrm{4}\right) \\ $$$$\mathrm{Adding}\:\left(\mathrm{3}\right)\:\mathrm{and}\:\left(\mathrm{4}\right) \\ $$$$\mathrm{x}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3}−\mathrm{9}^{\frac{\mathrm{1}}{\mathrm{3}}} \right) \\ $$$$\mathrm{Substracting}\:\left(\mathrm{4}\right)\mathrm{from}\:\left(\mathrm{3}\right) \\ $$$$\mathrm{y}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3}+\mathrm{9}^{\frac{\mathrm{1}}{\mathrm{3}}} \right) \\ $$$$ \\ $$

Commented by gunawan last updated on 08/Jun/19