Question Number 26625 by Leong last updated on 27/Dec/17
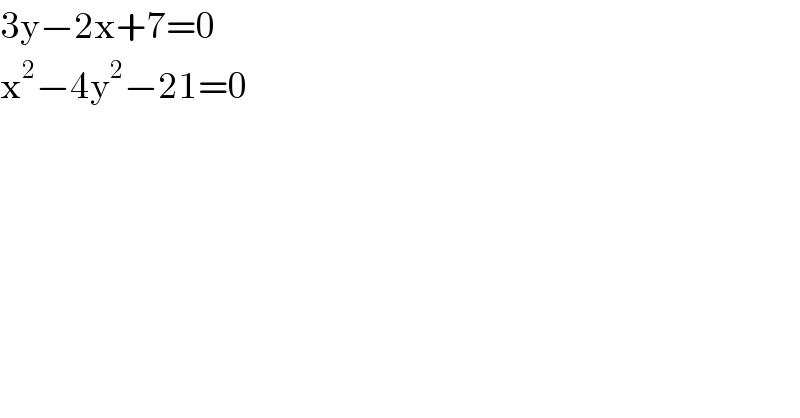
$$\mathrm{3y}−\mathrm{2x}+\mathrm{7}=\mathrm{0} \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{4y}^{\mathrm{2}} −\mathrm{21}=\mathrm{0} \\ $$
Answered by ajfour last updated on 27/Dec/17
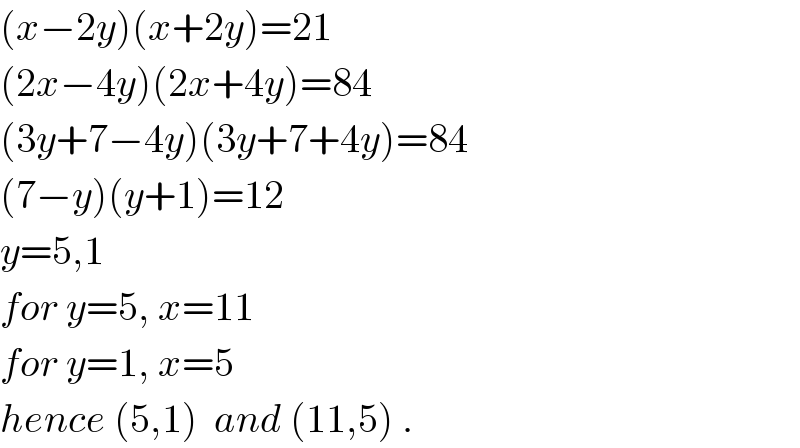
$$\left({x}−\mathrm{2}{y}\right)\left({x}+\mathrm{2}{y}\right)=\mathrm{21} \\ $$$$\left(\mathrm{2}{x}−\mathrm{4}{y}\right)\left(\mathrm{2}{x}+\mathrm{4}{y}\right)=\mathrm{84} \\ $$$$\left(\mathrm{3}{y}+\mathrm{7}−\mathrm{4}{y}\right)\left(\mathrm{3}{y}+\mathrm{7}+\mathrm{4}{y}\right)=\mathrm{84} \\ $$$$\left(\mathrm{7}−{y}\right)\left({y}+\mathrm{1}\right)=\mathrm{12} \\ $$$${y}=\mathrm{5},\mathrm{1} \\ $$$${for}\:{y}=\mathrm{5},\:{x}=\mathrm{11} \\ $$$${for}\:{y}=\mathrm{1},\:{x}=\mathrm{5} \\ $$$${hence}\:\left(\mathrm{5},\mathrm{1}\right)\:\:{and}\:\left(\mathrm{11},\mathrm{5}\right)\:. \\ $$
