Question Number 50795 by Gulay last updated on 20/Dec/18

$$\mathrm{4}+\frac{\mathrm{1}−\mathrm{3x}}{\mathrm{5}}=−\frac{\mathrm{x}−\mathrm{5}}{\mathrm{2}} \\ $$$$\mathrm{Sir}\:\mathrm{l}\:\mathrm{could}\:\mathrm{not}\:\mathrm{solve}\:\mathrm{this}\:\mathrm{question} \\ $$$$\mathrm{plz}\:\mathrm{help}\:\mathrm{me} \\ $$
Commented by hassentimol last updated on 20/Dec/18

$$\mathrm{4}+\left(\mathrm{1}/\mathrm{5}\right)−\left(\mathrm{3}/\mathrm{5}\right){x}=\left(−\mathrm{1}/\mathrm{2}\right){x}+\left(\mathrm{5}/\mathrm{2}\right) \\ $$$$\left(−\mathrm{1}/\mathrm{10}\right){x}=−\mathrm{17}/\mathrm{10} \\ $$$${x}=\mathrm{17} \\ $$$$\mathbb{S}\:=\:\left\{{x}\mid{x}=\mathrm{17}\right\} \\ $$
Answered by afachri last updated on 20/Dec/18
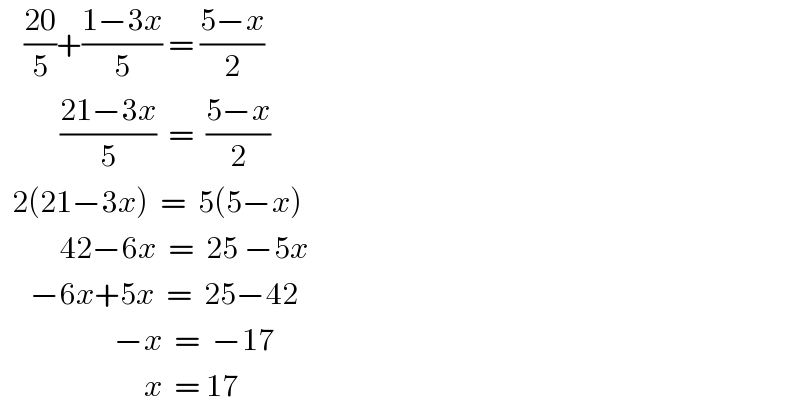
$$\:\:\:\:\frac{\mathrm{20}}{\mathrm{5}}+\frac{\mathrm{1}−\mathrm{3}{x}}{\mathrm{5}}\:=\:\frac{\mathrm{5}−{x}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{21}−\mathrm{3}{x}}{\mathrm{5}}\:\:=\:\:\frac{\mathrm{5}−{x}}{\mathrm{2}} \\ $$$$\:\:\mathrm{2}\left(\mathrm{21}−\mathrm{3}{x}\right)\:\:=\:\:\mathrm{5}\left(\mathrm{5}−{x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{42}−\mathrm{6}{x}\:\:=\:\:\mathrm{25}\:−\mathrm{5}{x} \\ $$$$\:\:\:\:\:−\mathrm{6}{x}+\mathrm{5}{x}\:\:=\:\:\mathrm{25}−\mathrm{42} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−{x}\:\:=\:\:−\mathrm{17} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}\:\:=\:\mathrm{17} \\ $$
Commented by Gulay last updated on 21/Dec/18

$$\mathrm{thamk}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{Sir} \\ $$
