Question Number 96171 by bemath last updated on 30/May/20
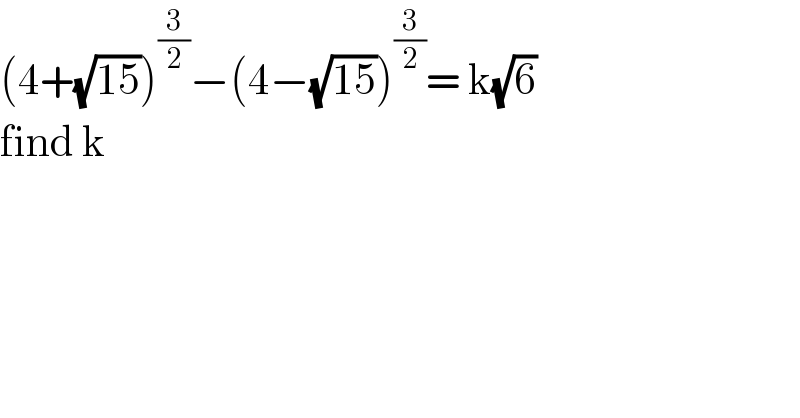
$$\left(\mathrm{4}+\sqrt{\mathrm{15}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\left(\mathrm{4}−\sqrt{\mathrm{15}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} =\:\mathrm{k}\sqrt{\mathrm{6}} \\ $$$$\mathrm{find}\:\mathrm{k}\: \\ $$
Commented by bobhans last updated on 30/May/20
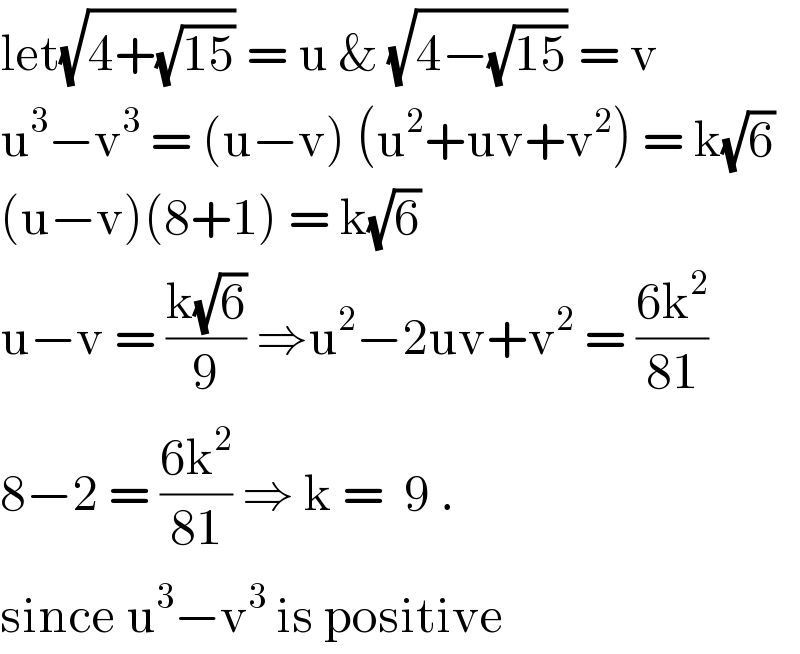
$$\mathrm{let}\sqrt{\mathrm{4}+\sqrt{\mathrm{15}}}\:=\:\mathrm{u}\:\&\:\sqrt{\mathrm{4}−\sqrt{\mathrm{15}}}\:=\:\mathrm{v}\: \\ $$$$\mathrm{u}^{\mathrm{3}} −\mathrm{v}^{\mathrm{3}} \:=\:\left(\mathrm{u}−\mathrm{v}\right)\:\left(\mathrm{u}^{\mathrm{2}} +\mathrm{uv}+\mathrm{v}^{\mathrm{2}} \right)\:=\:\mathrm{k}\sqrt{\mathrm{6}} \\ $$$$\left(\mathrm{u}−\mathrm{v}\right)\left(\mathrm{8}+\mathrm{1}\right)\:=\:\mathrm{k}\sqrt{\mathrm{6}}\: \\ $$$$\mathrm{u}−\mathrm{v}\:=\:\frac{\mathrm{k}\sqrt{\mathrm{6}}}{\mathrm{9}}\:\Rightarrow\mathrm{u}^{\mathrm{2}} −\mathrm{2uv}+\mathrm{v}^{\mathrm{2}} \:=\:\frac{\mathrm{6k}^{\mathrm{2}} }{\mathrm{81}} \\ $$$$\mathrm{8}−\mathrm{2}\:=\:\frac{\mathrm{6k}^{\mathrm{2}} }{\mathrm{81}}\:\Rightarrow\:\mathrm{k}\:=\:\:\mathrm{9}\:. \\ $$$$\mathrm{since}\:\mathrm{u}^{\mathrm{3}} −\mathrm{v}^{\mathrm{3}} \:\mathrm{is}\:\mathrm{positive} \\ $$
Commented by bemath last updated on 30/May/20

$$\mathrm{thanks} \\ $$
