Question Number 96311 by bemath last updated on 31/May/20
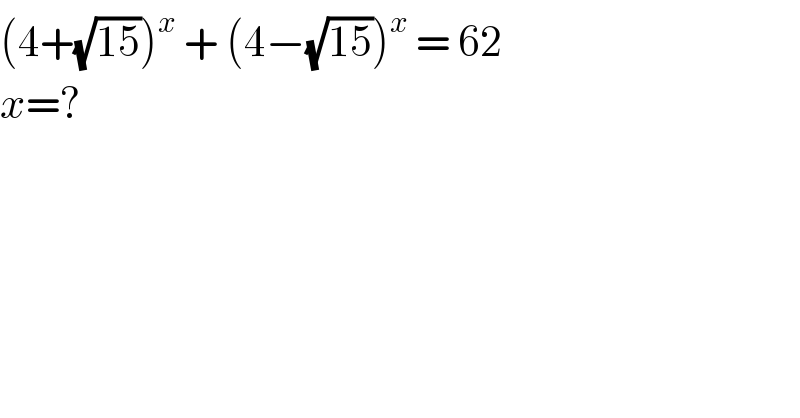
$$\left(\mathrm{4}+\sqrt{\mathrm{15}}\right)^{{x}} \:+\:\left(\mathrm{4}−\sqrt{\mathrm{15}}\right)^{{x}} \:=\:\mathrm{62}\: \\ $$$${x}=? \\ $$
Answered by bobhans last updated on 31/May/20
![4−(√(15)) × ((4+(√(15)))/(4+(√(15)))) = (1/(4+(√(15)))) so (4+(√(15)))^x + (1/((4+(√(15)))^x )) = 62 t + (1/t)−62 = 0 , [ t = (4+(√(15)))^x ] t^2 −62t+1 = 0 ⇒ t = ((62 + 16(√5))/2)= 31+8(√5) = (4+(√(15)))^2 = (4+(√(15)))^x , we get x = 2 the other root is (4+(√(15)))^(−2) = (4+(√(15)))^x x = −2](https://www.tinkutara.com/question/Q96312.png)
$$\mathrm{4}−\sqrt{\mathrm{15}}\:×\:\frac{\mathrm{4}+\sqrt{\mathrm{15}}}{\mathrm{4}+\sqrt{\mathrm{15}}}\:=\:\frac{\mathrm{1}}{\mathrm{4}+\sqrt{\mathrm{15}}} \\ $$$$\mathrm{so}\:\left(\mathrm{4}+\sqrt{\mathrm{15}}\right)^{{x}} +\:\frac{\mathrm{1}}{\left(\mathrm{4}+\sqrt{\mathrm{15}}\right)^{{x}} }\:=\:\mathrm{62}\: \\ $$$${t}\:+\:\frac{\mathrm{1}}{{t}}−\mathrm{62}\:=\:\mathrm{0}\:,\:\left[\:\mathrm{t}\:=\:\left(\mathrm{4}+\sqrt{\mathrm{15}}\right)^{{x}} \:\right] \\ $$$${t}^{\mathrm{2}} −\mathrm{62}{t}+\mathrm{1}\:=\:\mathrm{0}\:\Rightarrow\:\mathrm{t}\:=\:\frac{\mathrm{62}\:+\:\mathrm{16}\sqrt{\mathrm{5}}}{\mathrm{2}}=\:\mathrm{31}+\mathrm{8}\sqrt{\mathrm{5}} \\ $$$$=\:\left(\mathrm{4}+\sqrt{\mathrm{15}}\right)^{\mathrm{2}} \:=\:\left(\mathrm{4}+\sqrt{\mathrm{15}}\right)^{{x}} \:,\:\mathrm{we}\:\mathrm{get}\:{x}\:=\:\mathrm{2} \\ $$$${the}\:{other}\:{root}\:{is}\:\left(\mathrm{4}+\sqrt{\mathrm{15}}\right)^{−\mathrm{2}} \:=\:\left(\mathrm{4}+\sqrt{\mathrm{15}}\right)^{{x}} \\ $$$${x}\:=\:−\mathrm{2}\: \\ $$$$ \\ $$
