Question Number 85711 by Rio Michael last updated on 24/Mar/20
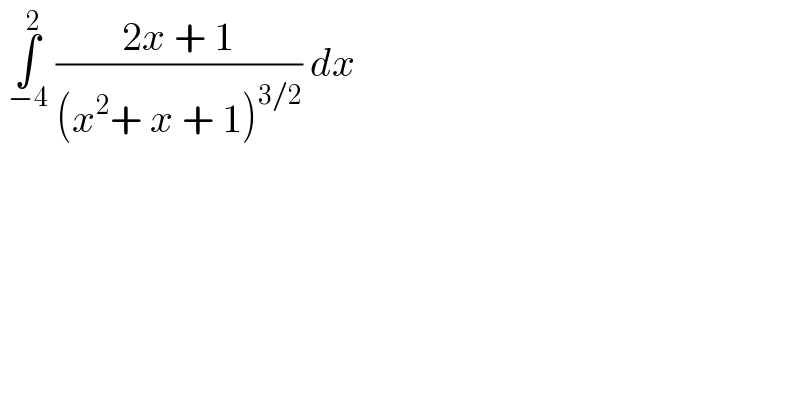
$$\:\underset{−\mathrm{4}} {\overset{\mathrm{2}} {\int}}\:\frac{\mathrm{2}{x}\:+\:\mathrm{1}}{\left({x}^{\mathrm{2}} +\:{x}\:+\:\mathrm{1}\right)^{\mathrm{3}/\mathrm{2}} }\:{dx} \\ $$
Commented by jagoll last updated on 24/Mar/20
![∫_(−4) ^2 ((d(x^2 +x+1))/((x^2 +x+1)^(3/2) )) = [−(2/( (√(x^2 +x+1)))) ]^2 _( −4) = −(2/( (√7))) + (2/( (√(13))))](https://www.tinkutara.com/question/Q85712.png)
$$\underset{−\mathrm{4}} {\overset{\mathrm{2}} {\int}}\:\frac{\mathrm{d}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}/\mathrm{2}} }\: \\ $$$$=\:\left[−\frac{\mathrm{2}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}\:\underset{\:\:−\mathrm{4}} {\right]}^{\mathrm{2}} \\ $$$$=\:−\frac{\mathrm{2}}{\:\sqrt{\mathrm{7}}}\:+\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{13}}} \\ $$
Commented by Rio Michael last updated on 24/Mar/20

$$\mathrm{great} \\ $$
