Menu Close

4-2x-2-8-x-

Tinku Tara 0 Comments
Pin




Question Number 29433 by Victor31926 last updated on 08/Feb/18
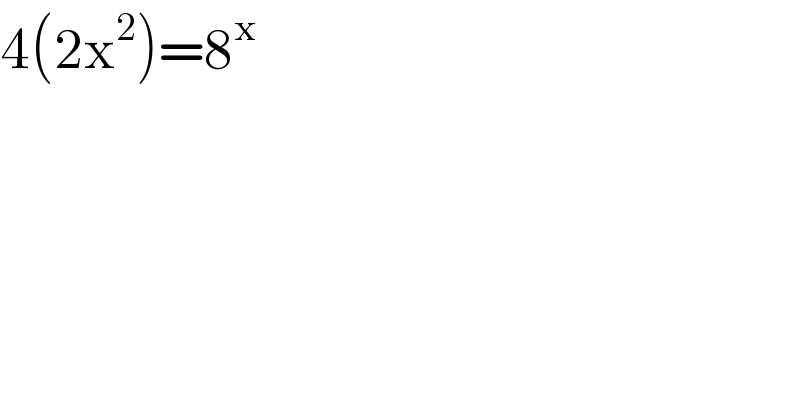
4(2x^2 )=8^x
$$\mathrm{4}\left(\mathrm{2x}^{\mathrm{2}} \right)=\mathrm{8}^{\mathrm{x}} \\ $$
Answered by mrW2 last updated on 08/Feb/18
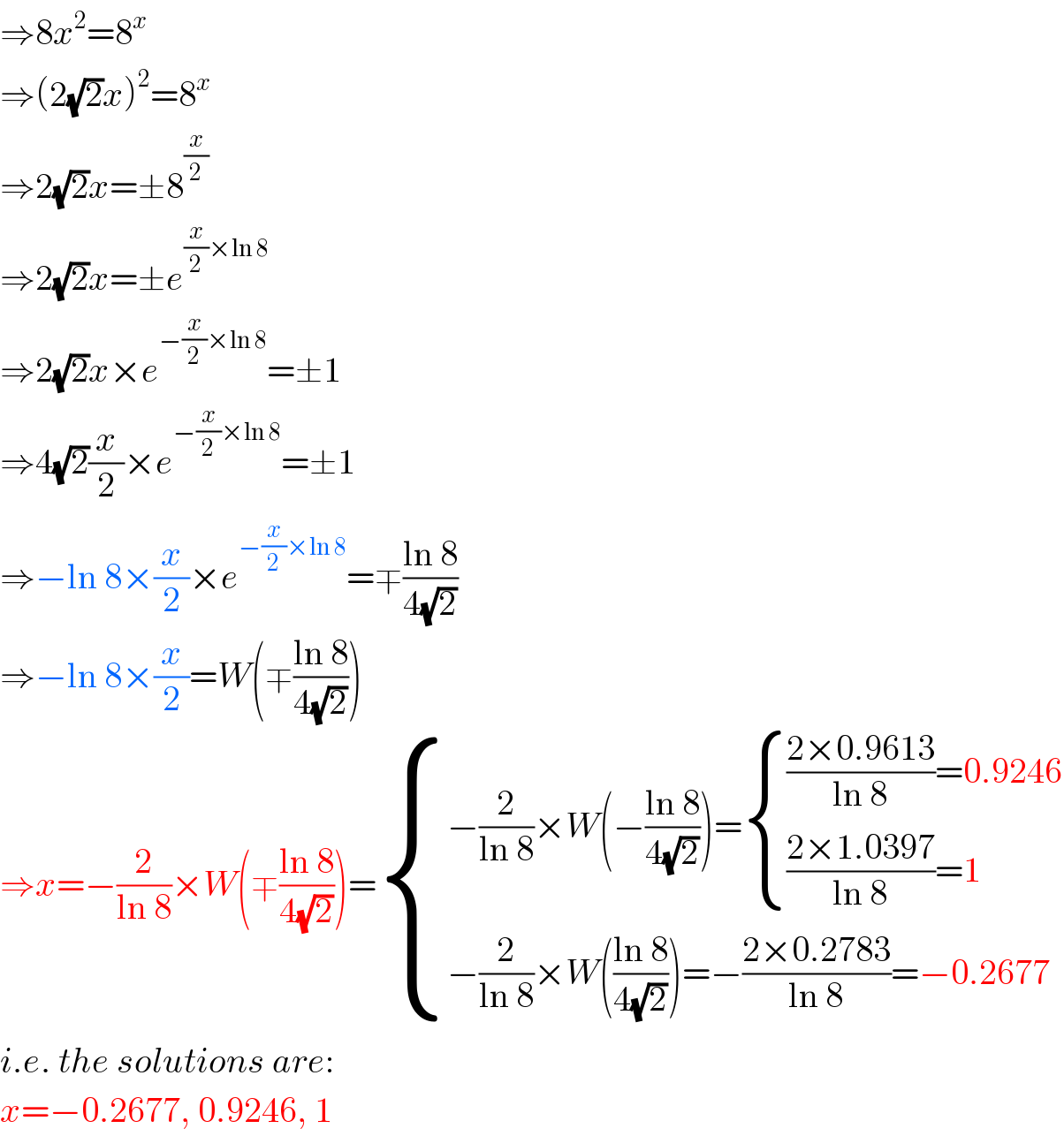
⇒8x^2 =8^x ⇒(2(√2)x)^2 =8^x ⇒2(√2)x=±8^(x/2) ⇒2(√2)x=±e^((x/2)×ln 8) ⇒2(√2)x×e^(−(x/2)×ln 8) =±1 ⇒4(√2)(x/2)×e^(−(x/2)×ln 8) =±1 ⇒−ln 8×(x/2)×e^(−(x/2)×ln 8) =∓((ln 8)/(4(√2))) ⇒−ln 8×(x/2)=W(∓((ln 8)/(4(√2)))) ⇒x=−(2/(ln 8))×W(∓((ln 8)/(4(√2))))= { ((−(2/(ln 8))×W(−((ln 8)/(4(√2))))= { ((((2×0.9613)/(ln 8))=0.9246)),((((2×1.0397)/(ln 8))=1)) :})),((−(2/(ln 8))×W(((ln 8)/(4(√2))))=−((2×0.2783)/(ln 8))=−0.2677)) :} i.e. the solutions are: x=−0.2677, 0.9246, 1
$$\Rightarrow\mathrm{8}{x}^{\mathrm{2}} =\mathrm{8}^{{x}} \\ $$$$\Rightarrow\left(\mathrm{2}\sqrt{\mathrm{2}}{x}\right)^{\mathrm{2}} =\mathrm{8}^{{x}} \\ $$$$\Rightarrow\mathrm{2}\sqrt{\mathrm{2}}{x}=\pm\mathrm{8}^{\frac{{x}}{\mathrm{2}}} \\ $$$$\Rightarrow\mathrm{2}\sqrt{\mathrm{2}}{x}=\pm{e}^{\frac{{x}}{\mathrm{2}}×\mathrm{ln}\:\mathrm{8}} \\ $$$$\Rightarrow\mathrm{2}\sqrt{\mathrm{2}}{x}×{e}^{−\frac{{x}}{\mathrm{2}}×\mathrm{ln}\:\mathrm{8}} =\pm\mathrm{1} \\ $$$$\Rightarrow\mathrm{4}\sqrt{\mathrm{2}}\frac{{x}}{\mathrm{2}}×{e}^{−\frac{{x}}{\mathrm{2}}×\mathrm{ln}\:\mathrm{8}} =\pm\mathrm{1} \\ $$$$\Rightarrow−\mathrm{ln}\:\mathrm{8}×\frac{{x}}{\mathrm{2}}×{e}^{−\frac{{x}}{\mathrm{2}}×\mathrm{ln}\:\mathrm{8}} =\mp\frac{\mathrm{ln}\:\mathrm{8}}{\mathrm{4}\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow−\mathrm{ln}\:\mathrm{8}×\frac{{x}}{\mathrm{2}}={W}\left(\mp\frac{\mathrm{ln}\:\mathrm{8}}{\mathrm{4}\sqrt{\mathrm{2}}}\right) \\ $$$$\Rightarrow{x}=−\frac{\mathrm{2}}{\mathrm{ln}\:\mathrm{8}}×{W}\left(\mp\frac{\mathrm{ln}\:\mathrm{8}}{\mathrm{4}\sqrt{\mathrm{2}}}\right)=\begin{cases}{−\frac{\mathrm{2}}{\mathrm{ln}\:\mathrm{8}}×{W}\left(−\frac{\mathrm{ln}\:\mathrm{8}}{\mathrm{4}\sqrt{\mathrm{2}}}\right)=\begin{cases}{\frac{\mathrm{2}×\mathrm{0}.\mathrm{9613}}{\mathrm{ln}\:\mathrm{8}}=\mathrm{0}.\mathrm{9246}}\\{\frac{\mathrm{2}×\mathrm{1}.\mathrm{0397}}{\mathrm{ln}\:\mathrm{8}}=\mathrm{1}}\end{cases}}\\{−\frac{\mathrm{2}}{\mathrm{ln}\:\mathrm{8}}×{W}\left(\frac{\mathrm{ln}\:\mathrm{8}}{\mathrm{4}\sqrt{\mathrm{2}}}\right)=−\frac{\mathrm{2}×\mathrm{0}.\mathrm{2783}}{\mathrm{ln}\:\mathrm{8}}=−\mathrm{0}.\mathrm{2677}}\end{cases} \\ $$$${i}.{e}.\:{the}\:{solutions}\:{are}: \\ $$$${x}=−\mathrm{0}.\mathrm{2677},\:\mathrm{0}.\mathrm{9246},\:\mathrm{1} \\ $$
Commented by Victor31926 last updated on 08/Feb/18
wow...thanks a lot.
$$\mathrm{wow}…\mathrm{thanks}\:\mathrm{a}\:\mathrm{lot}. \\ $$
Commented by Victor31926 last updated on 08/Feb/18
pls explain wat dat W stands for.
$$\mathrm{pls}\:\mathrm{explain}\:\mathrm{wat}\:\mathrm{dat}\:\mathrm{W}\:\mathrm{stands}\:\mathrm{for}. \\ $$
Commented by mrW2 last updated on 08/Feb/18
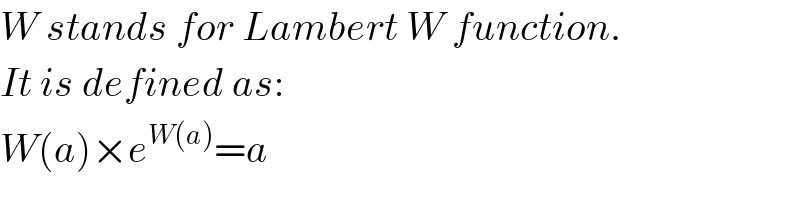
W stands for Lambert W function. It is defined as: W(a)×e^(W(a)) =a
$${W}\:{stands}\:{for}\:{Lambert}\:{W}\:{function}. \\ $$$${It}\:{is}\:{defined}\:{as}: \\ $$$${W}\left({a}\right)×{e}^{{W}\left({a}\right)} ={a} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *