Question Number 117258 by Dwaipayan Shikari last updated on 10/Oct/20

$$\frac{\mathrm{4}}{\mathrm{3}}.\frac{\mathrm{9}}{\mathrm{8}}.\frac{\mathrm{49}}{\mathrm{48}}.\frac{\mathrm{121}}{\mathrm{120}}.\frac{\mathrm{169}}{\mathrm{168}}.\frac{\mathrm{289}}{\mathrm{288}}.\frac{\mathrm{529}}{\mathrm{528}}.\frac{\mathrm{831}}{\mathrm{830}}…..\infty \\ $$
Answered by AbduraufKodiriy last updated on 10/Oct/20

$$−\begin{cases}{\boldsymbol{\zeta}\left(\mathrm{2}\right)=\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+…}\\{\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\boldsymbol{\zeta}\left(\mathrm{2}\right)=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{6}^{\mathrm{2}} }+…}\end{cases}\Rightarrow\:\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\right)\boldsymbol{\zeta}\left(\mathrm{2}\right)=\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{7}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{9}^{\mathrm{2}} }+…\:\Rightarrow \\ $$$$\Rightarrow\:−\begin{cases}{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\right)\boldsymbol{\zeta}\left(\mathrm{2}\right)=\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{2}} }+…}\\{\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\right)\boldsymbol{\zeta}\left(\mathrm{2}\right)=\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{9}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{15}^{\mathrm{2}} }+…}\end{cases}\Rightarrow \\ $$$$\Rightarrow\:\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\right)\boldsymbol{\zeta}\left(\mathrm{2}\right)=\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{7}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{11}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{13}^{\mathrm{2}} }+… \\ $$$$………………………… \\ $$$$\boldsymbol{\zeta}\left(\mathrm{2}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{2}} }\right)…=\mathrm{1} \\ $$$$\frac{\pi^{\mathrm{2}} }{\mathrm{6}}=\frac{\mathrm{2}^{\mathrm{2}} }{\mathrm{2}^{\mathrm{2}} −\mathrm{1}}\centerdot\frac{\mathrm{3}^{\mathrm{2}} }{\mathrm{3}^{\mathrm{2}} −\mathrm{1}}\centerdot\frac{\mathrm{5}^{\mathrm{2}} }{\mathrm{5}^{\mathrm{2}} −\mathrm{1}}\centerdot\frac{\mathrm{7}^{\mathrm{2}} }{\mathrm{7}^{\mathrm{2}} −\mathrm{1}}\centerdot… \\ $$$$\frac{\pi^{\mathrm{2}} }{\mathrm{6}}=\frac{\mathrm{4}}{\mathrm{3}}\centerdot\frac{\mathrm{9}}{\mathrm{8}}\centerdot\frac{\mathrm{25}}{\mathrm{24}}\centerdot\frac{\mathrm{49}}{\mathrm{48}}\centerdot…\:\Rightarrow\:\frac{\mathrm{4}\pi^{\mathrm{2}} }{\mathrm{25}}=\frac{\mathrm{4}}{\mathrm{3}}\centerdot\frac{\mathrm{9}}{\mathrm{8}}\centerdot\frac{\mathrm{49}}{\mathrm{48}}\centerdot\frac{\mathrm{121}}{\mathrm{120}}\centerdot… \\ $$
Commented by Dwaipayan Shikari last updated on 10/Oct/20
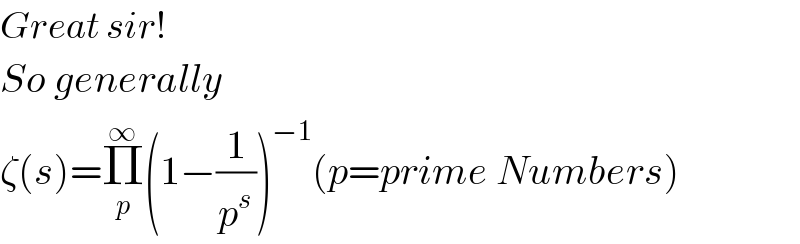
$${Great}\:{sir}! \\ $$$${So}\:{generally} \\ $$$$\zeta\left({s}\right)=\underset{{p}} {\overset{\infty} {\prod}}\left(\mathrm{1}−\frac{\mathrm{1}}{{p}^{{s}} }\right)^{−\mathrm{1}} \left({p}={prime}\:{Numbers}\right) \\ $$
