Question Number 119773 by bemath last updated on 26/Oct/20
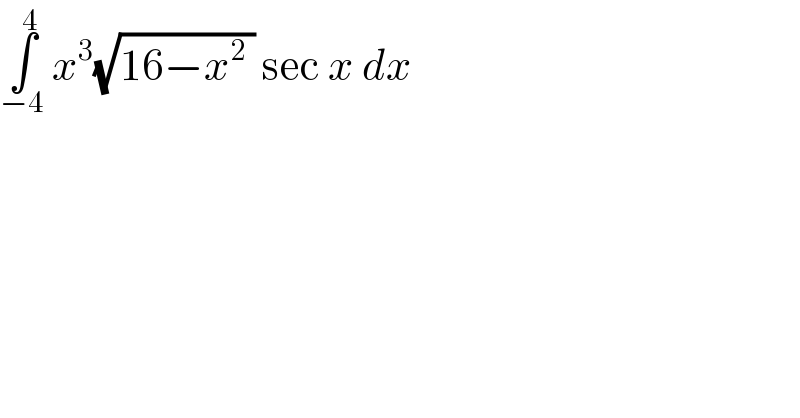
$$\underset{−\mathrm{4}} {\overset{\mathrm{4}} {\int}}\:{x}^{\mathrm{3}} \sqrt{\mathrm{16}−{x}^{\mathrm{2}} \:}\:\mathrm{sec}\:{x}\:{dx}\: \\ $$
Answered by MJS_new last updated on 27/Oct/20
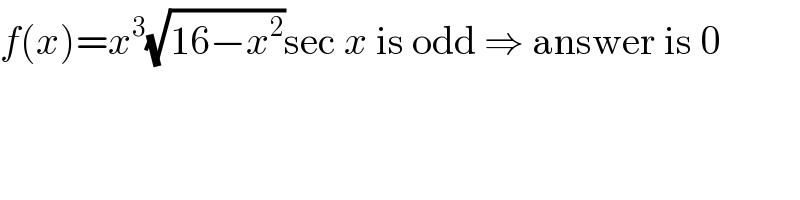
$${f}\left({x}\right)={x}^{\mathrm{3}} \sqrt{\mathrm{16}−{x}^{\mathrm{2}} }\mathrm{sec}\:{x}\:\mathrm{is}\:\mathrm{odd}\:\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\mathrm{0} \\ $$
Answered by john santu last updated on 27/Oct/20
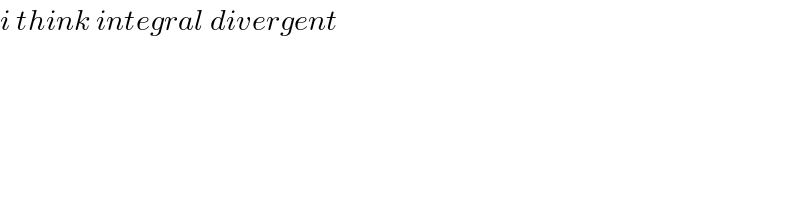
$${i}\:{think}\:{integral}\:{divergent} \\ $$
Answered by mathmax by abdo last updated on 27/Oct/20

$$\mathrm{if}\:\mathrm{sec}\:\mathrm{x}=\frac{\mathrm{1}}{\mathrm{cosx}}\:\Rightarrow\int_{−\mathrm{4}} ^{\mathrm{4}} \frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{cosx}}\sqrt{\mathrm{16}−\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:=\mathrm{0} \\ $$$$\mathrm{becsuse}\:\mathrm{the}\:\mathrm{function}\:\mathrm{under}\:\mathrm{integral}\:\mathrm{is}\:\mathrm{odd} \\ $$
