Question Number 20201 by khamizan833@gmail.con last updated on 24/Aug/17
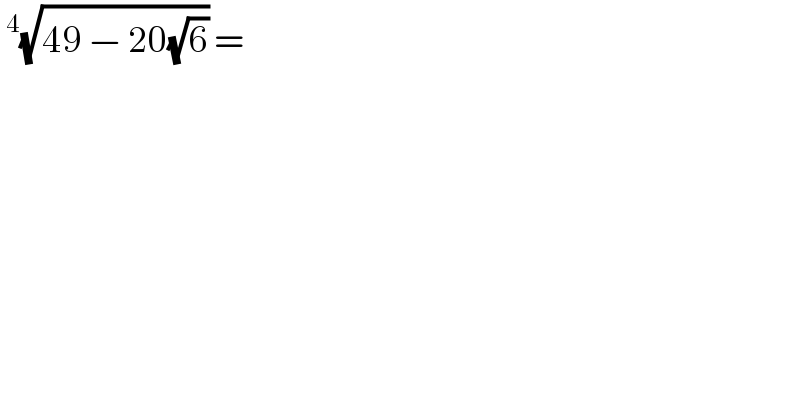
$$\:^{\mathrm{4}} \sqrt{\mathrm{49}\:−\:\mathrm{20}\sqrt{\mathrm{6}}}\:= \\ $$
Answered by Einstein Newton last updated on 24/Aug/17

$$\sqrt{\mathrm{49}\:−\:\mathrm{20}\sqrt{\mathrm{6}}}\:=\:\sqrt{\mathrm{5}^{\mathrm{2}} \:+\:\left(\mathrm{2}\sqrt{\mathrm{6}}\right)^{\mathrm{2}} \:−\:\mathrm{2}\left(\mathrm{5}\right)\left(\mathrm{2}\sqrt{\mathrm{6}}\right)} \\ $$$$=\:\mathrm{5}\:−\:\mathrm{2}\sqrt{\mathrm{6}} \\ $$$$\mathrm{Now}\:\sqrt{\mathrm{5}\:−\:\mathrm{2}\sqrt{\mathrm{6}}}\:=\:\sqrt{\mathrm{3}}\:−\:\sqrt{\mathrm{2}} \\ $$$$\therefore\:\sqrt[{\mathrm{4}}]{\mathrm{49}\:−\:\mathrm{20}\sqrt{\mathrm{6}}}\:=\:\sqrt{\mathrm{3}}\:−\:\sqrt{\mathrm{2}} \\ $$
Answered by $@ty@m last updated on 24/Aug/17

$$\therefore\sqrt{\mathrm{40}−\mathrm{20}\sqrt{\mathrm{6}}}=\mathrm{5}−\sqrt{\mathrm{24}} \\ $$$$\Rightarrow{x}^{\mathrm{2}} +{y}=\mathrm{49}\:\&\:\mathrm{2}{x}\sqrt{{y}}=\mathrm{20}\sqrt{\mathrm{6}} \\ $$$$\Rightarrow{x}^{\mathrm{2}} +{y}=\mathrm{49}\:\&\:{x}^{\mathrm{2}} {y}=\mathrm{600} \\ $$$$\Rightarrow\frac{\mathrm{600}}{{y}}+{y}=\mathrm{49} \\ $$$$\Rightarrow{y}^{\mathrm{2}} −\mathrm{49}{y}+\mathrm{600}=\mathrm{0} \\ $$$$\Rightarrow{y}=\frac{\mathrm{49}\pm\sqrt{\mathrm{2401}−\mathrm{2400}}}{\mathrm{2}} \\ $$$$\Rightarrow{y}=\frac{\mathrm{49}\pm\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{y}=\mathrm{25},\mathrm{24} \\ $$$$\Rightarrow{x}=\sqrt{\mathrm{24}},\:\sqrt{\mathrm{25}} \\ $$$$\therefore\sqrt{\mathrm{40}−\mathrm{20}\sqrt{\mathrm{6}}}=\pm\left(\mathrm{5}−\sqrt{\mathrm{24}}\right) \\ $$$${again}, \\ $$$${let}\:\sqrt{\mathrm{5}−\sqrt{\mathrm{24}}}={u}−\sqrt{{v}}\: \\ $$$${proceeding}\:{in}\:{the}\:{same}\:{manner} \\ $$$${we}\:{get}\:{u}=\sqrt{\mathrm{3}},\sqrt{\mathrm{2}},\:{v}=\mathrm{2},\mathrm{3} \\ $$$$\therefore\:^{\mathrm{4}} \sqrt{\mathrm{49}−\mathrm{20}\sqrt{\mathrm{6}}}=\pm\left(\sqrt{\mathrm{3}}−\sqrt{\left.\mathrm{2}\right)},\:\pm\left(\sqrt{\mathrm{3}}−\sqrt{\left.\mathrm{2}\right)}\right.\right. \\ $$$$\left({nth}\:{root}\:{of}\:\mathrm{49}−\mathrm{20}\sqrt{\mathrm{6}\:}{will}\:{have}\:{n}\:{roots}.\right) \\ $$
