Question Number 168537 by Mastermind last updated on 12/Apr/22
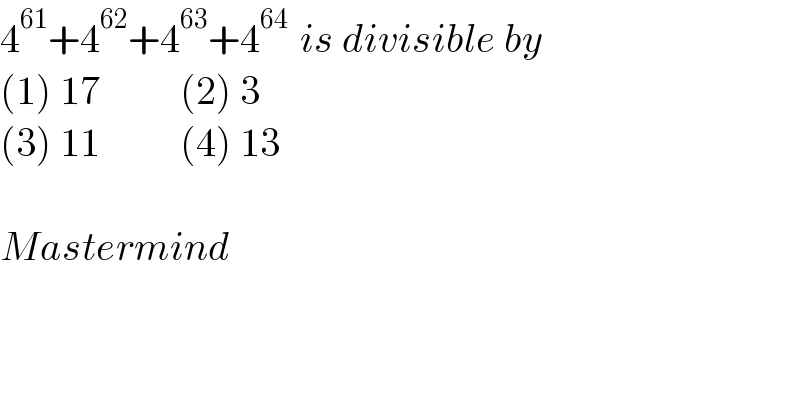
$$\mathrm{4}^{\mathrm{61}} +\mathrm{4}^{\mathrm{62}} +\mathrm{4}^{\mathrm{63}} +\mathrm{4}^{\mathrm{64}\:} \:{is}\:{divisible}\:{by} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{17}\:\:\:\:\:\:\:\:\:\:\left(\mathrm{2}\right)\:\mathrm{3} \\ $$$$\left(\mathrm{3}\right)\:\mathrm{11}\:\:\:\:\:\:\:\:\:\:\left(\mathrm{4}\right)\:\mathrm{13} \\ $$$$ \\ $$$${Mastermind} \\ $$
Answered by MJS_new last updated on 12/Apr/22
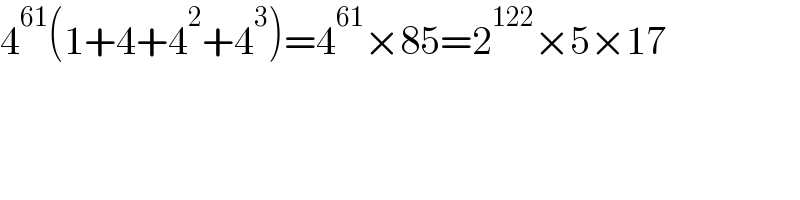
$$\mathrm{4}^{\mathrm{61}} \left(\mathrm{1}+\mathrm{4}+\mathrm{4}^{\mathrm{2}} +\mathrm{4}^{\mathrm{3}} \right)=\mathrm{4}^{\mathrm{61}} ×\mathrm{85}=\mathrm{2}^{\mathrm{122}} ×\mathrm{5}×\mathrm{17} \\ $$
Answered by mathfreak last updated on 12/Apr/22
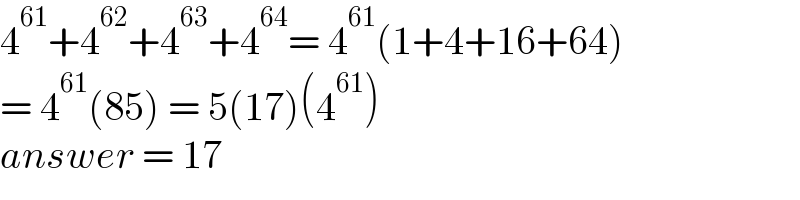
$$\mathrm{4}^{\mathrm{61}} +\mathrm{4}^{\mathrm{62}} +\mathrm{4}^{\mathrm{63}} +\mathrm{4}^{\mathrm{64}} =\:\mathrm{4}^{\mathrm{61}} \left(\mathrm{1}+\mathrm{4}+\mathrm{16}+\mathrm{64}\right) \\ $$$$=\:\mathrm{4}^{\mathrm{61}} \left(\mathrm{85}\right)\:=\:\mathrm{5}\left(\mathrm{17}\right)\left(\mathrm{4}^{\mathrm{61}} \right) \\ $$$${answer}\:=\:\mathrm{17} \\ $$
