Question Number 126499 by liberty last updated on 21/Dec/20
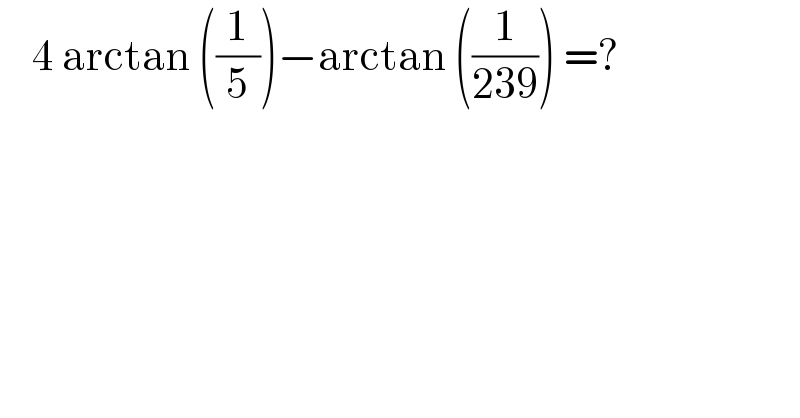
$$\:\:\:\:\mathrm{4}\:\mathrm{arctan}\:\left(\frac{\mathrm{1}}{\mathrm{5}}\right)−\mathrm{arctan}\:\left(\frac{\mathrm{1}}{\mathrm{239}}\right)\:=? \\ $$
Answered by benjo_mathlover last updated on 21/Dec/20
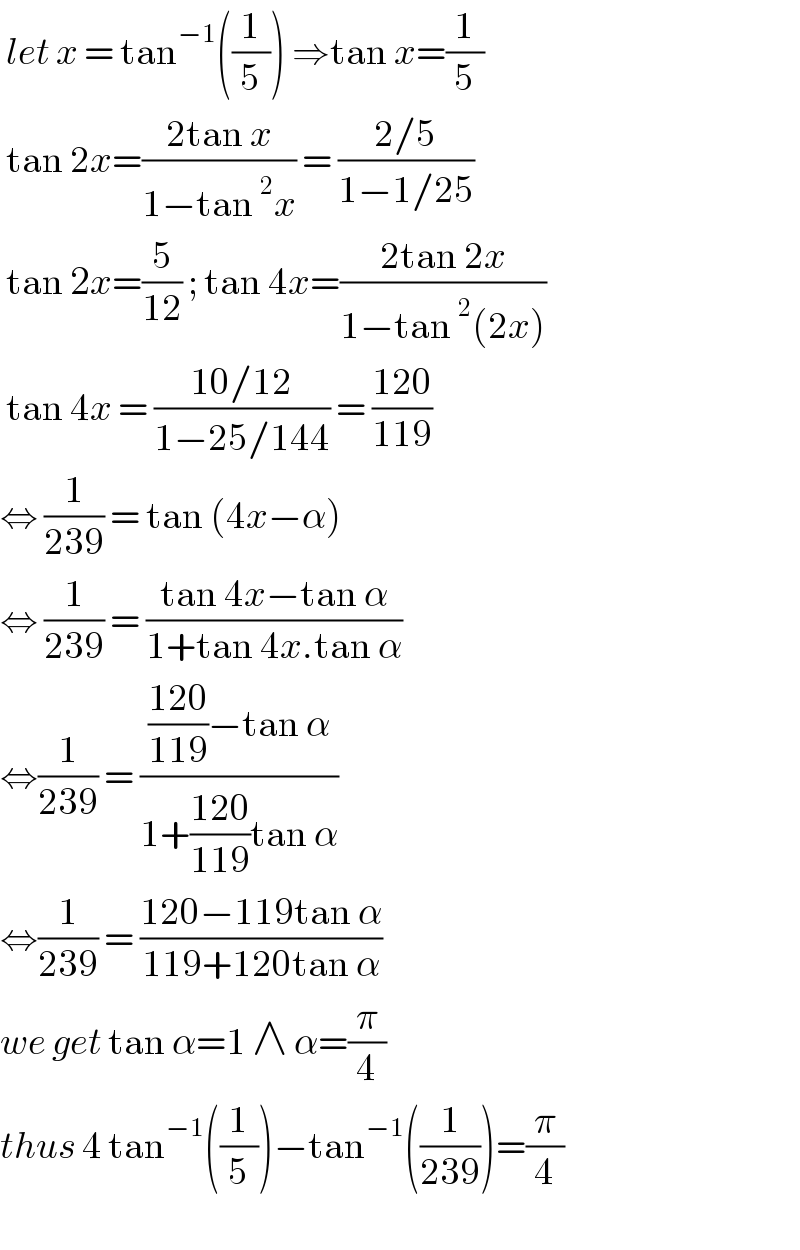
$$\:{let}\:{x}\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{5}}\right)\:\Rightarrow\mathrm{tan}\:{x}=\frac{\mathrm{1}}{\mathrm{5}} \\ $$$$\:\mathrm{tan}\:\mathrm{2}{x}=\frac{\mathrm{2tan}\:{x}}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} {x}}\:=\:\frac{\mathrm{2}/\mathrm{5}}{\mathrm{1}−\mathrm{1}/\mathrm{25}}\: \\ $$$$\:\mathrm{tan}\:\mathrm{2}{x}=\frac{\mathrm{5}}{\mathrm{12}}\:;\:\mathrm{tan}\:\mathrm{4}{x}=\frac{\mathrm{2tan}\:\mathrm{2}{x}}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \left(\mathrm{2}{x}\right)} \\ $$$$\:\mathrm{tan}\:\mathrm{4}{x}\:=\:\frac{\mathrm{10}/\mathrm{12}}{\mathrm{1}−\mathrm{25}/\mathrm{144}}\:=\:\frac{\mathrm{120}}{\mathrm{119}} \\ $$$$\Leftrightarrow\:\frac{\mathrm{1}}{\mathrm{239}}\:=\:\mathrm{tan}\:\left(\mathrm{4}{x}−\alpha\right) \\ $$$$\Leftrightarrow\:\frac{\mathrm{1}}{\mathrm{239}}\:=\:\frac{\mathrm{tan}\:\mathrm{4}{x}−\mathrm{tan}\:\alpha}{\mathrm{1}+\mathrm{tan}\:\mathrm{4}{x}.\mathrm{tan}\:\alpha} \\ $$$$\Leftrightarrow\frac{\mathrm{1}}{\mathrm{239}}\:=\:\frac{\frac{\mathrm{120}}{\mathrm{119}}−\mathrm{tan}\:\alpha}{\mathrm{1}+\frac{\mathrm{120}}{\mathrm{119}}\mathrm{tan}\:\alpha} \\ $$$$\Leftrightarrow\frac{\mathrm{1}}{\mathrm{239}}\:=\:\frac{\mathrm{120}−\mathrm{119tan}\:\alpha}{\mathrm{119}+\mathrm{120tan}\:\alpha} \\ $$$${we}\:{get}\:\mathrm{tan}\:\alpha=\mathrm{1}\:\wedge\:\alpha=\frac{\pi}{\mathrm{4}} \\ $$$${thus}\:\mathrm{4}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{5}}\right)−\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{239}}\right)=\frac{\pi}{\mathrm{4}} \\ $$$$ \\ $$
