4-cos-50-1-sin-20-

Question Number 146261 by mathdanisur last updated on 12/Jul/21

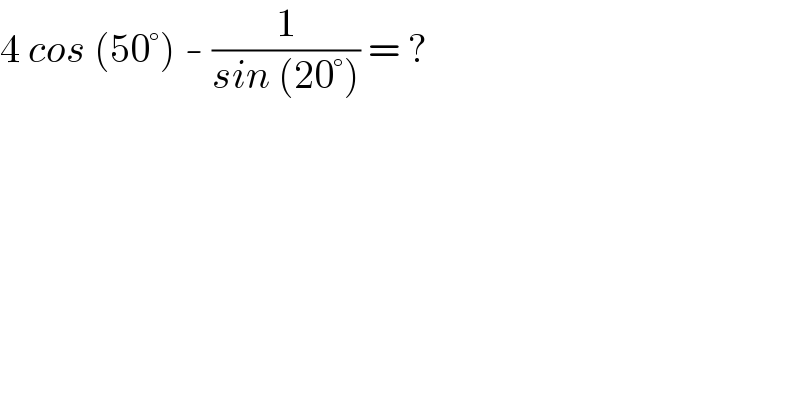
$$\mathrm{4}\:{cos}\:\left(\mathrm{50}°\right)\:-\:\frac{\mathrm{1}}{{sin}\:\left(\mathrm{20}°\right)}\:=\:? \\ $$

Answered by bemath last updated on 12/Jul/21

((4cos 50°.cos 70°−1)/(sin 20°)) = ((2(cos 120°+cos 20°)−1)/(sin 20°)) = ((−1+2cos 20°−1)/(sin 20°)) = ((2(cos 20°−1))/(sin 20°)) = ((−4sin^2 10°)/(sin 20°)) =−2tan 10°

$$\:\frac{\mathrm{4cos}\:\mathrm{50}°.\mathrm{cos}\:\mathrm{70}°−\mathrm{1}}{\mathrm{sin}\:\mathrm{20}°}\:= \\ $$$$\:\frac{\mathrm{2}\left(\mathrm{cos}\:\mathrm{120}°+\mathrm{cos}\:\mathrm{20}°\right)−\mathrm{1}}{\mathrm{sin}\:\mathrm{20}°}\:= \\ $$$$\:\frac{−\mathrm{1}+\mathrm{2cos}\:\mathrm{20}°−\mathrm{1}}{\mathrm{sin}\:\mathrm{20}°}\:=\: \\ $$$$\:\frac{\mathrm{2}\left(\mathrm{cos}\:\mathrm{20}°−\mathrm{1}\right)}{\mathrm{sin}\:\mathrm{20}°}\:=\:\frac{−\mathrm{4sin}\:^{\mathrm{2}} \mathrm{10}°}{\mathrm{sin}\:\mathrm{20}°} \\ $$$$=−\mathrm{2tan}\:\mathrm{10}°\: \\ $$

Commented by iloveisrael last updated on 13/Jul/21

=−((2(1−2sin^2 10−1))/(2sin 10° cos 10°)) =−2((sin 10°)/(cos 10°))=−2tan 10°

$$=−\frac{\cancel{\mathrm{2}}\left(\cancel{\mathrm{1}}−\mathrm{2sin}\:^{\mathrm{2}} \mathrm{10}\cancel{−\mathrm{1}}\right)}{\cancel{\mathrm{2}sin}\:\mathrm{10}°\:\mathrm{cos}\:\mathrm{10}°} \\ $$$$=−\mathrm{2}\frac{\mathrm{sin}\:\mathrm{10}°}{\mathrm{cos}\:\mathrm{10}°}=−\mathrm{2tan}\:\mathrm{10}°\: \\ $$

Commented by mathdanisur last updated on 12/Jul/21

$${cool}\:{thanks}\:{Ser} \\ $$

Commented by mathdanisur last updated on 12/Jul/21

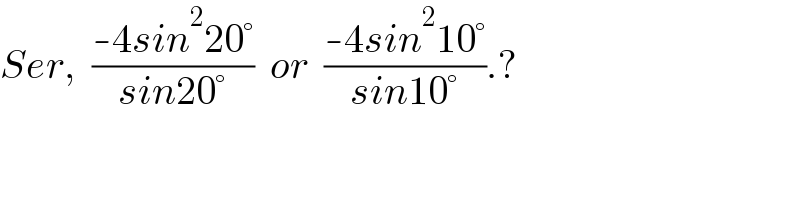
Ser, ((-4sin^2 20°)/(sin20°)) or ((-4sin^2 10°)/(sin10°)).?

$${Ser},\:\:\frac{-\mathrm{4}{sin}^{\mathrm{2}} \mathrm{20}°}{{sin}\mathrm{20}°}\:\:{or}\:\:\frac{-\mathrm{4}{sin}^{\mathrm{2}} \mathrm{10}°}{{sin}\mathrm{10}°}.? \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply