Question Number 117163 by bemath last updated on 10/Oct/20
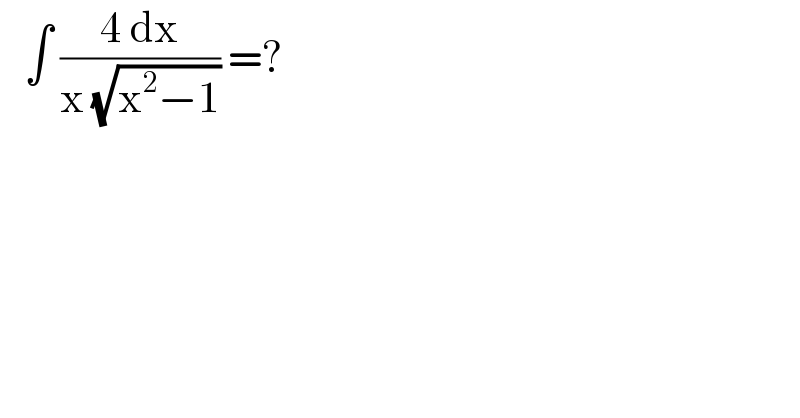
$$\:\:\:\int\:\frac{\mathrm{4}\:\mathrm{dx}}{\mathrm{x}\:\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}}\:=? \\ $$
Answered by bemath last updated on 10/Oct/20
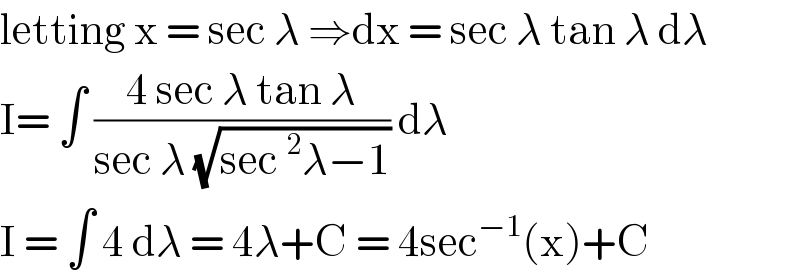
$$\mathrm{letting}\:\mathrm{x}\:=\:\mathrm{sec}\:\lambda\:\Rightarrow\mathrm{dx}\:=\:\mathrm{sec}\:\lambda\:\mathrm{tan}\:\lambda\:\mathrm{d}\lambda \\ $$$$\mathrm{I}=\:\int\:\frac{\mathrm{4}\:\mathrm{sec}\:\lambda\:\mathrm{tan}\:\lambda}{\mathrm{sec}\:\lambda\:\sqrt{\mathrm{sec}\:^{\mathrm{2}} \lambda−\mathrm{1}}}\:\mathrm{d}\lambda \\ $$$$\mathrm{I}\:=\:\int\:\mathrm{4}\:\mathrm{d}\lambda\:=\:\mathrm{4}\lambda+\mathrm{C}\:=\:\mathrm{4sec}^{−\mathrm{1}} \left(\mathrm{x}\right)+\mathrm{C} \\ $$
Answered by Dwaipayan Shikari last updated on 10/Oct/20
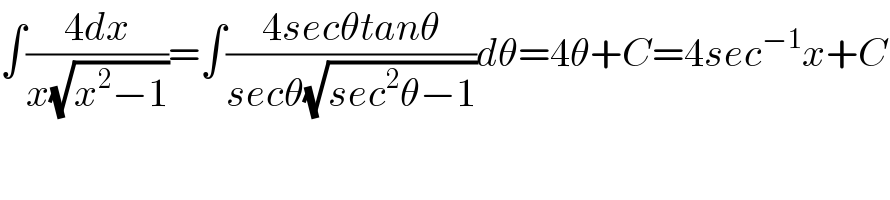
$$\int\frac{\mathrm{4}{dx}}{{x}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}=\int\frac{\mathrm{4}{sec}\theta{tan}\theta}{{sec}\theta\sqrt{{sec}^{\mathrm{2}} \theta−\mathrm{1}}}{d}\theta=\mathrm{4}\theta+{C}=\mathrm{4}{sec}^{−\mathrm{1}} {x}+{C} \\ $$
