Question Number 151804 by abdurehime last updated on 23/Aug/21

Answered by amin96 last updated on 23/Aug/21

Commented by MJS_new last updated on 23/Aug/21

Answered by MJS_new last updated on 23/Aug/21
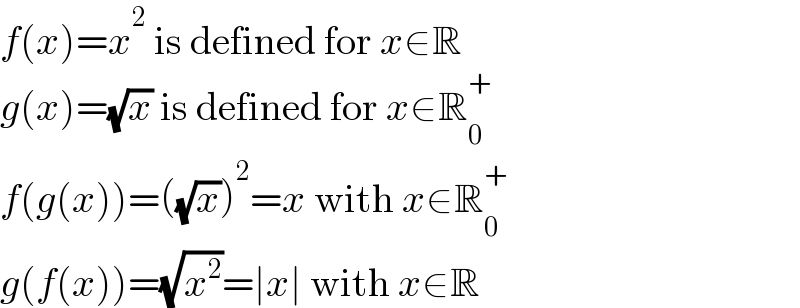
Commented by abdurehime last updated on 23/Aug/21

Commented by MJS_new last updated on 23/Aug/21

Commented by abdurehime last updated on 23/Aug/21

Commented by otchereabdullai@gmail.com last updated on 23/Aug/21

