Question Number 116966 by bobhans last updated on 08/Oct/20
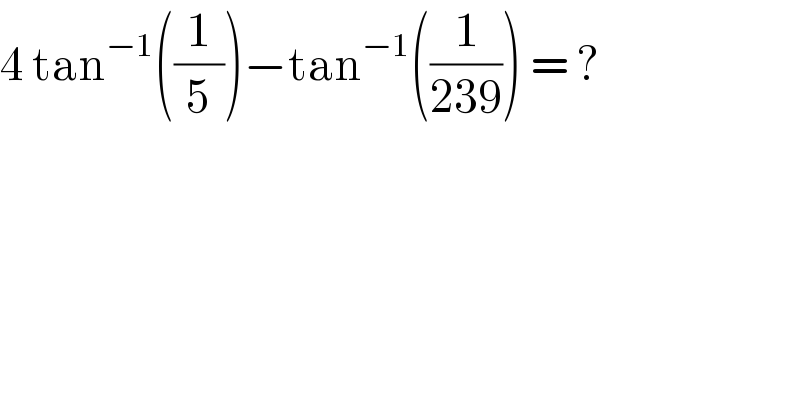
$$\mathrm{4}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{5}}\right)−\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{239}}\right)\:=\:? \\ $$
Answered by bemath last updated on 08/Oct/20
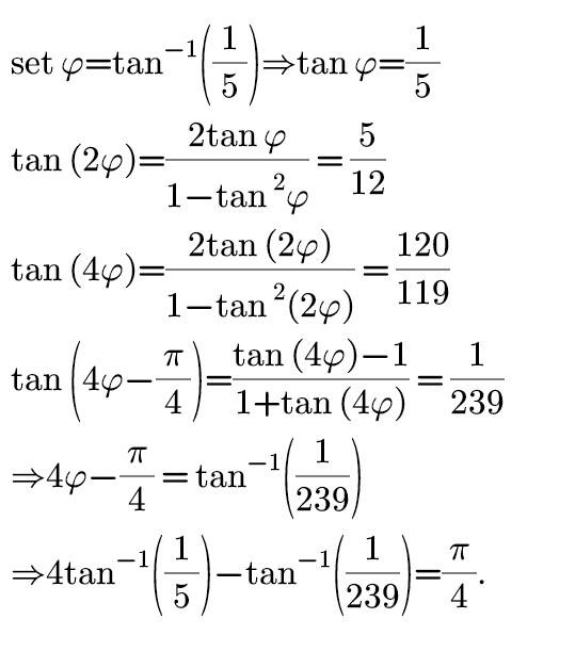
Answered by TANMAY PANACEA last updated on 08/Oct/20

$$\mathrm{2}{tan}^{−\mathrm{1}} \left(\frac{\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{5}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{5}}×\frac{\mathrm{1}}{\mathrm{5}}}\right)−{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{239}}\right) \\ $$$$=\mathrm{2}{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}×\mathrm{25}}{\mathrm{5}×\mathrm{24}}\right)−{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{239}}\right) \\ $$$$={tan}^{−\mathrm{1}} \left(\frac{\frac{\mathrm{5}}{\mathrm{12}}+\frac{\mathrm{5}}{\mathrm{12}}}{\mathrm{1}−\frac{\mathrm{25}}{\mathrm{144}}}\right)−{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{239}}\right) \\ $$$$={tan}^{−\mathrm{1}} \left(\frac{\mathrm{10}}{\mathrm{12}}×\frac{\mathrm{144}}{\mathrm{119}}\right)−{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{239}}\right) \\ $$$$={tan}^{−\mathrm{1}} \left(\frac{\frac{\mathrm{120}}{\mathrm{119}}−\frac{\mathrm{1}}{\mathrm{239}}}{\mathrm{1}+\frac{\mathrm{120}×\mathrm{1}}{\mathrm{119}×\mathrm{239}}}\right)={tan}^{−\mathrm{1}} \left(\frac{\mathrm{120}×\mathrm{239}−\mathrm{119}}{\mathrm{119}×\mathrm{239}+\mathrm{120}}\right) \\ $$$$={tan}^{−\mathrm{1}} \left(\frac{\mathrm{119}×\mathrm{239}+\mathrm{239}−\mathrm{119}}{\mathrm{119}×\mathrm{239}+\mathrm{120}}\right)={tan}^{−\mathrm{1}} \left(\frac{\mathrm{119}×\mathrm{239}+\mathrm{120}}{\mathrm{119}×\mathrm{239}+\mathrm{120}}\right) \\ $$$$={tan}^{−\mathrm{1}} \left(\mathrm{1}\right)=\frac{\pi}{\mathrm{4}} \\ $$
