Question Number 112145 by weltr last updated on 06/Sep/20
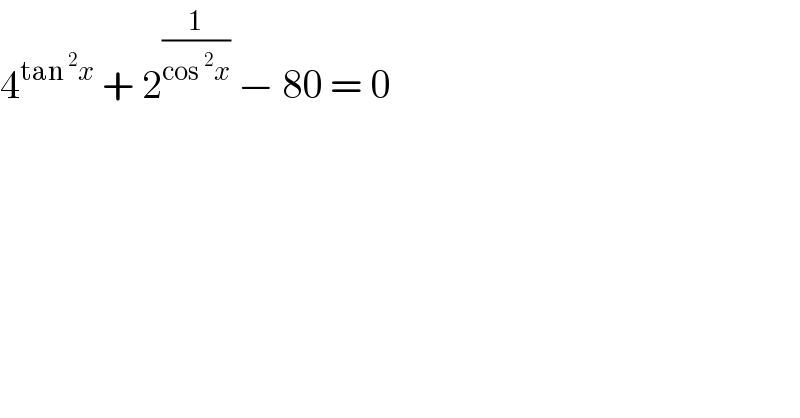
$$\mathrm{4}^{\mathrm{tan}\:^{\mathrm{2}} {x}} \:+\:\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{cos}\:^{\mathrm{2}} {x}}} \:−\:\mathrm{80}\:=\:\mathrm{0} \\ $$
Answered by bemath last updated on 06/Sep/20
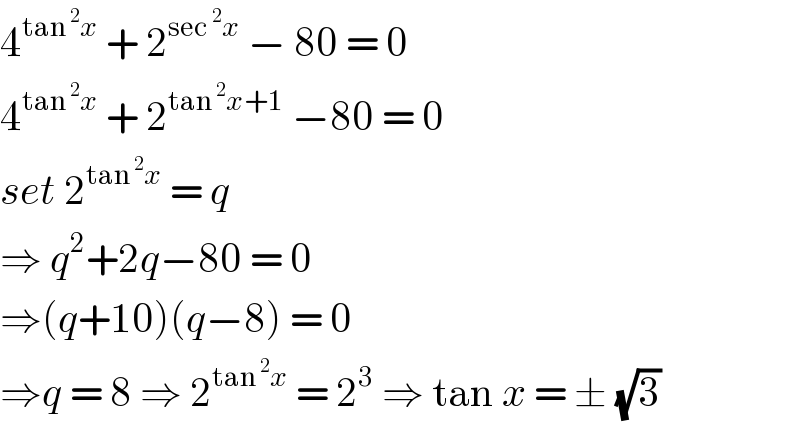
$$\mathrm{4}^{\mathrm{tan}\:^{\mathrm{2}} {x}} \:+\:\mathrm{2}^{\mathrm{sec}\:^{\mathrm{2}} {x}} \:−\:\mathrm{80}\:=\:\mathrm{0} \\ $$$$\mathrm{4}^{\mathrm{tan}\:^{\mathrm{2}} {x}} \:+\:\mathrm{2}^{\mathrm{tan}\:^{\mathrm{2}} {x}+\mathrm{1}} \:−\mathrm{80}\:=\:\mathrm{0} \\ $$$${set}\:\mathrm{2}^{\mathrm{tan}\:^{\mathrm{2}} {x}} \:=\:{q} \\ $$$$\Rightarrow\:{q}^{\mathrm{2}} +\mathrm{2}{q}−\mathrm{80}\:=\:\mathrm{0} \\ $$$$\Rightarrow\left({q}+\mathrm{10}\right)\left({q}−\mathrm{8}\right)\:=\:\mathrm{0} \\ $$$$\Rightarrow{q}\:=\:\mathrm{8}\:\Rightarrow\:\mathrm{2}^{\mathrm{tan}\:^{\mathrm{2}} {x}} \:=\:\mathrm{2}^{\mathrm{3}} \:\Rightarrow\:\mathrm{tan}\:{x}\:=\:\pm\:\sqrt{\mathrm{3}} \\ $$
Commented by weltr last updated on 06/Sep/20
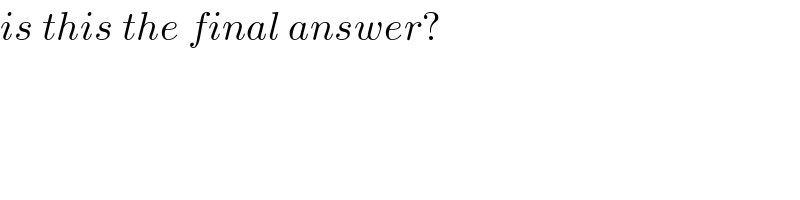
$${is}\:{this}\:{the}\:{final}\:{answer}? \\ $$
Commented by bobhans last updated on 06/Sep/20
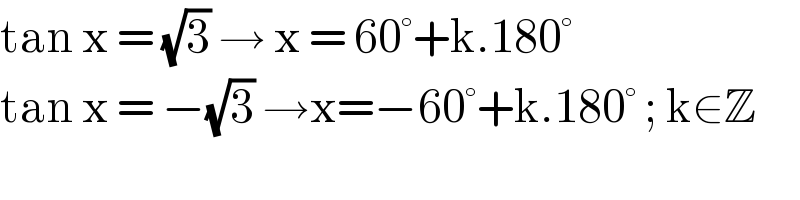
$$\mathrm{tan}\:\mathrm{x}\:=\:\sqrt{\mathrm{3}}\:\rightarrow\:\mathrm{x}\:=\:\mathrm{60}°+\mathrm{k}.\mathrm{180}° \\ $$$$\mathrm{tan}\:\mathrm{x}\:=\:−\sqrt{\mathrm{3}}\:\rightarrow\mathrm{x}=−\mathrm{60}°+\mathrm{k}.\mathrm{180}°\:;\:\mathrm{k}\in\mathbb{Z} \\ $$
Commented by weltr last updated on 07/Sep/20

$${thanks} \\ $$
