Question Number 85362 by sahnaz last updated on 21/Mar/20

$$\int\frac{−\mathrm{4}−\mathrm{u}}{\mathrm{u}^{\mathrm{2}} +\mathrm{5u}+\mathrm{6}}\mathrm{du} \\ $$
Answered by john santu last updated on 22/Mar/20
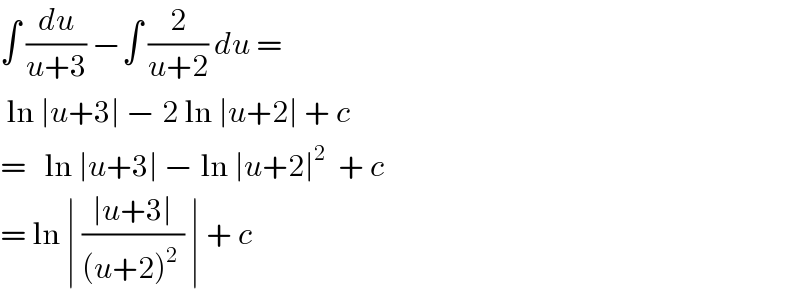
$$\int\:\frac{{du}}{{u}+\mathrm{3}}\:−\int\:\frac{\mathrm{2}}{{u}+\mathrm{2}}\:{du}\:=\: \\ $$$$\:\mathrm{ln}\:\mid{u}+\mathrm{3}\mid\:−\:\mathrm{2}\:\mathrm{ln}\:\mid{u}+\mathrm{2}\mid\:+\:{c}\: \\ $$$$=\:\:\:\mathrm{ln}\:\mid{u}+\mathrm{3}\mid\:−\:\mathrm{ln}\:\mid{u}+\mathrm{2}\mid^{\mathrm{2}} \:\:+\:{c} \\ $$$$=\:\mathrm{ln}\:\mid\:\frac{\mid{u}+\mathrm{3}\mid}{\left({u}+\mathrm{2}\right)^{\mathrm{2}} \:}\:\mid\:+\:{c} \\ $$
Commented by MJS last updated on 21/Mar/20
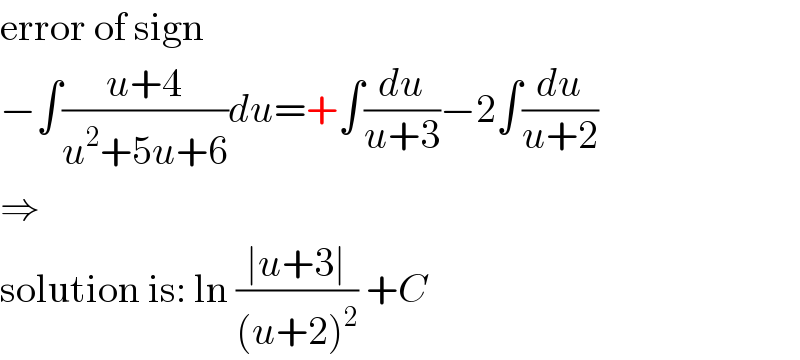
$$\mathrm{error}\:\mathrm{of}\:\mathrm{sign} \\ $$$$−\int\frac{{u}+\mathrm{4}}{{u}^{\mathrm{2}} +\mathrm{5}{u}+\mathrm{6}}{du}=+\int\frac{{du}}{{u}+\mathrm{3}}−\mathrm{2}\int\frac{{du}}{{u}+\mathrm{2}} \\ $$$$\Rightarrow \\ $$$$\mathrm{solution}\:\mathrm{is}:\:\mathrm{ln}\:\frac{\mid{u}+\mathrm{3}\mid}{\left({u}+\mathrm{2}\right)^{\mathrm{2}} }\:+{C} \\ $$
Commented by sahnaz last updated on 21/Mar/20

$$\mathrm{yes}\:\:\mathrm{thank}\:\mathrm{you} \\ $$
