Question Number 47532 by 143jesus last updated on 11/Nov/18

$$\sqrt{\mathrm{400}^{\mathrm{2}} +\mathrm{100}^{\mathrm{2}=} } \\ $$
Answered by Joel578 last updated on 11/Nov/18
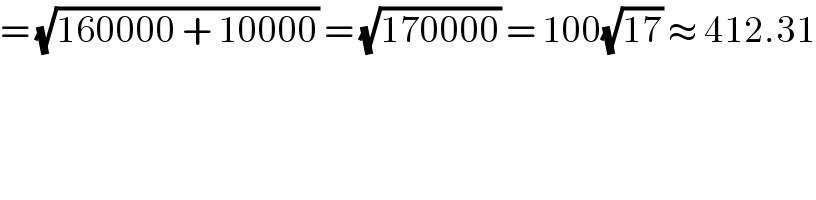
$$=\:\sqrt{\mathrm{160000}\:+\:\mathrm{10000}}\:=\:\sqrt{\mathrm{170000}}\:=\:\mathrm{100}\sqrt{\mathrm{17}}\:\approx\:\mathrm{412}.\mathrm{31} \\ $$
Answered by arcana last updated on 11/Nov/18
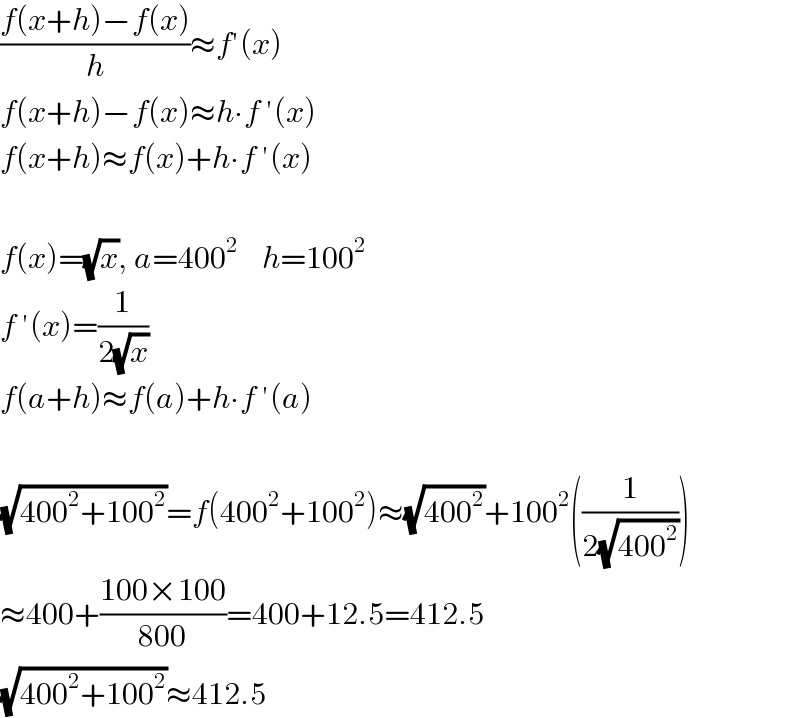
$$\frac{{f}\left({x}+{h}\right)−{f}\left({x}\right)}{{h}}\approx{f}'\left({x}\right) \\ $$$${f}\left({x}+{h}\right)−{f}\left({x}\right)\approx{h}\centerdot{f}\:'\left({x}\right) \\ $$$${f}\left({x}+{h}\right)\approx{f}\left({x}\right)+{h}\centerdot{f}\:'\left({x}\right) \\ $$$$ \\ $$$${f}\left({x}\right)=\sqrt{{x}},\:{a}=\mathrm{400}^{\mathrm{2}} \:\:\:\:{h}=\mathrm{100}^{\mathrm{2}} \\ $$$${f}\:'\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}} \\ $$$${f}\left({a}+{h}\right)\approx{f}\left({a}\right)+{h}\centerdot{f}\:'\left({a}\right) \\ $$$$ \\ $$$$\sqrt{\mathrm{400}^{\mathrm{2}} +\mathrm{100}^{\mathrm{2}} }={f}\left(\mathrm{400}^{\mathrm{2}} +\mathrm{100}^{\mathrm{2}} \right)\approx\sqrt{\mathrm{400}^{\mathrm{2}} }+\mathrm{100}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{400}^{\mathrm{2}} }}\right) \\ $$$$\approx\mathrm{400}+\frac{\mathrm{100}×\mathrm{100}}{\mathrm{800}}=\mathrm{400}+\mathrm{12}.\mathrm{5}=\mathrm{412}.\mathrm{5} \\ $$$$\sqrt{\mathrm{400}^{\mathrm{2}} +\mathrm{100}^{\mathrm{2}} }\approx\mathrm{412}.\mathrm{5} \\ $$
