Question Number 171085 by balirampatel last updated on 07/Jun/22
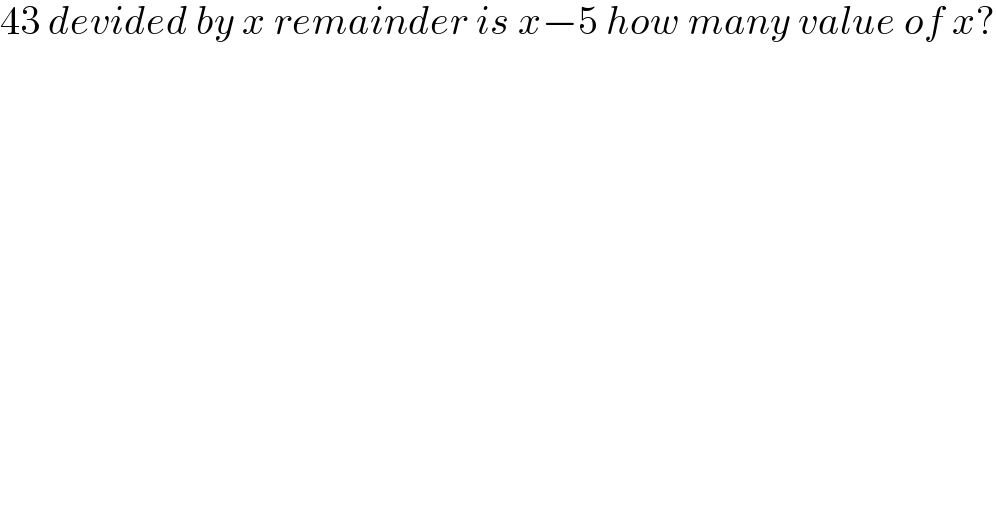
$$\mathrm{43}\:{devided}\:{by}\:{x}\:{remainder}\:{is}\:{x}−\mathrm{5}\:{how}\:{many}\:{value}\:{of}\:{x}? \\ $$
Answered by Rasheed.Sindhi last updated on 08/Jun/22

$$ \\ $$$${Assuming}: \\ $$$$\:\:\mathrm{1}<{divisor}<\mathrm{43}\:\wedge\:\mathrm{0}\leqslant{remainder}<\mathrm{43} \\ $$$$\:\:\mathrm{1}<{x}<\mathrm{43}\:\wedge\:\mathrm{0}\leqslant{x}−\mathrm{5}<\mathrm{43} \\ $$$$\:\bullet\:\mathrm{5}\leqslant{x}<\mathrm{43}…………………\left(\mathrm{i}\right) \\ $$$$\frac{\mathrm{43}−\left({x}−\mathrm{5}\right)}{{x}}={m}\in\mathbb{N} \\ $$$$\mathrm{48}−{x}={mx} \\ $$$$\bullet\left({m}+\mathrm{1}\right){x}=\mathrm{48}\Rightarrow{x}\:\mid\:\mathrm{48}……..\left(\mathrm{ii}\right) \\ $$$${from}\:\left(\mathrm{i}\right)\:\&\:\left(\mathrm{ii}\right): \\ $$$${x}=\mathrm{6},\mathrm{8},\mathrm{12},\mathrm{16},\mathrm{24} \\ $$$$\begin{array}{|c|c|c|c|c|c|}{\underset{{x}} {{divisor}}}&\hline{\underset{{x}−\mathrm{5}} {{remainder}}}\\{\:\:\:\:\:\:\mathrm{6}}&\hline{\:\:\:\:\:\:\:\:\:\:\mathrm{1}}\\{\:\:\:\:\:\:\mathrm{8}}&\hline{\:\:\:\:\:\:\:\:\:\:\mathrm{3}}\\{\:\:\:\:\mathrm{12}}&\hline{\:\:\:\:\:\:\:\:\:\:\mathrm{7}}\\{\:\:\:\:\mathrm{16}}&\hline{\:\:\:\:\:\:\:\:\mathrm{11}}\\{\:\:\:\:\mathrm{24}}&\hline{\:\:\:\:\:\:\:\:\mathrm{19}}\\\hline\end{array} \\ $$
Commented by balirampatel last updated on 08/Jun/22

$${Thanks}\:{Sir} \\ $$
