Question Number 122484 by JBocanegra last updated on 17/Nov/20
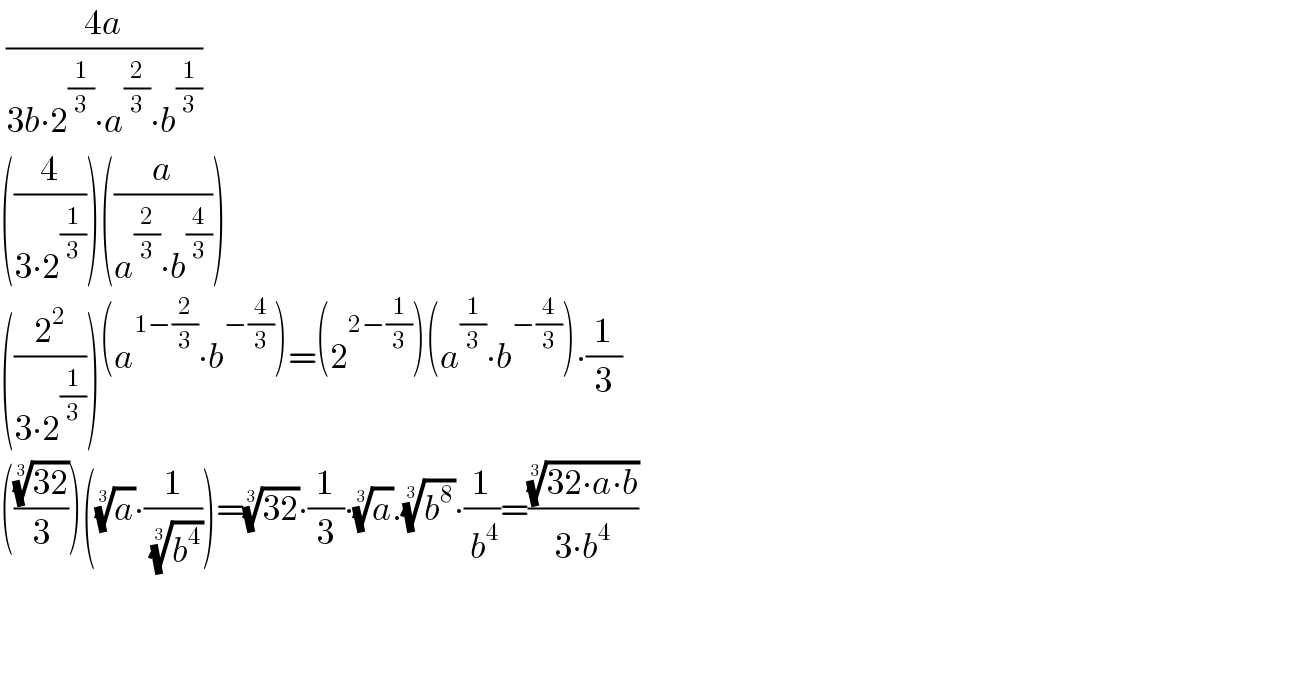
$$\:\frac{\mathrm{4}{a}}{\mathrm{3}{b}\centerdot\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{3}}} \centerdot{a}^{\frac{\mathrm{2}}{\mathrm{3}}} \centerdot{b}^{\frac{\mathrm{1}}{\mathrm{3}}} } \\ $$$$\left(\frac{\mathrm{4}}{\mathrm{3}\centerdot\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{3}}} }\right)\left(\frac{{a}}{{a}^{\frac{\mathrm{2}}{\mathrm{3}}} \centerdot{b}^{\frac{\mathrm{4}}{\mathrm{3}}} }\right) \\ $$$$\left(\frac{\mathrm{2}^{\mathrm{2}} }{\mathrm{3}\centerdot\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{3}}} }\right)\left({a}^{\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3}}} \centerdot{b}^{−\frac{\mathrm{4}}{\mathrm{3}}} \right)=\left(\mathrm{2}^{\mathrm{2}−\frac{\mathrm{1}}{\mathrm{3}}} \right)\left({a}^{\frac{\mathrm{1}}{\mathrm{3}}} \centerdot{b}^{−\frac{\mathrm{4}}{\mathrm{3}}} \right)\centerdot\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\left(\frac{\sqrt[{\mathrm{3}}]{\mathrm{32}}}{\mathrm{3}}\right)\left(\sqrt[{\mathrm{3}}]{{a}}\centerdot\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{{b}^{\mathrm{4}} }}\right)=\sqrt[{\mathrm{3}}]{\mathrm{32}}\centerdot\frac{\mathrm{1}}{\mathrm{3}}\centerdot\sqrt[{\mathrm{3}}]{{a}}.\sqrt[{\mathrm{3}}]{{b}^{\mathrm{8}} }\centerdot\frac{\mathrm{1}}{\:{b}^{\mathrm{4}} }=\frac{\sqrt[{\mathrm{3}}]{\mathrm{32}\centerdot{a}\centerdot{b}}}{\mathrm{3}\centerdot{b}^{\mathrm{4}} } \\ $$$$ \\ $$$$ \\ $$
