Question Number 162951 by Ar Brandon last updated on 02/Jan/22

$$\mathrm{4men}\:\mathrm{clear}\:\mathrm{a}\:\mathrm{farm}\:\mathrm{for}\:\mathrm{8}\:\mathrm{days}\:\mathrm{and}\:\mathrm{are}\:\mathrm{paid}\:\mathrm{24\$} \\ $$$$\mathrm{How}\:\mathrm{long}\:\mathrm{will}\:\mathrm{6}\:\mathrm{men}\:\mathrm{take}\:\mathrm{to}\:\mathrm{clear}\:\mathrm{the}\:\mathrm{same}\:\mathrm{farm} \\ $$$$\mathrm{if}\:\mathrm{they}\:\mathrm{are}\:\mathrm{paid}\:\mathrm{360\$}\:? \\ $$
Commented by mr W last updated on 03/Jan/22

$$\mathrm{4}\:{men}\:{earn}\:{in}\:\mathrm{8}\:{days}\:\mathrm{24\$}.\:\Rightarrow{one}\:{man}\:{in}\:{one}\:{day}:\:\frac{\mathrm{24}}{\mathrm{4}×\mathrm{8}} \\ $$$$\mathrm{6}\:{men}\:{earn}\:{in}\:{x}\:{days}\:\mathrm{360\$}.\:\Rightarrow{one}\:{man}\:{in}\:{one}\:{day}:\:\frac{\mathrm{360}}{\mathrm{6}{x}} \\ $$$${since}\:{it}'{s}\:{a}\:{constant}\:{how}\:{much}\:{one}\:{man} \\ $$$${earns}\:{in}\:{one}\:{day}\:\left({we}\:{must}\:{assume},\right. \\ $$$$\left.{otherwise}\:{not}\:{solvable}\right), \\ $$$$\frac{\mathrm{24}}{\mathrm{4}×\mathrm{8}}=\frac{\mathrm{360}}{\mathrm{6}{x}} \\ $$$$\Rightarrow{x}=\mathrm{80}\:{days} \\ $$
Commented by Ar Brandon last updated on 03/Jan/22
Got it now. Thanks Sir.
Answered by Rasheed.Sindhi last updated on 02/Jan/22
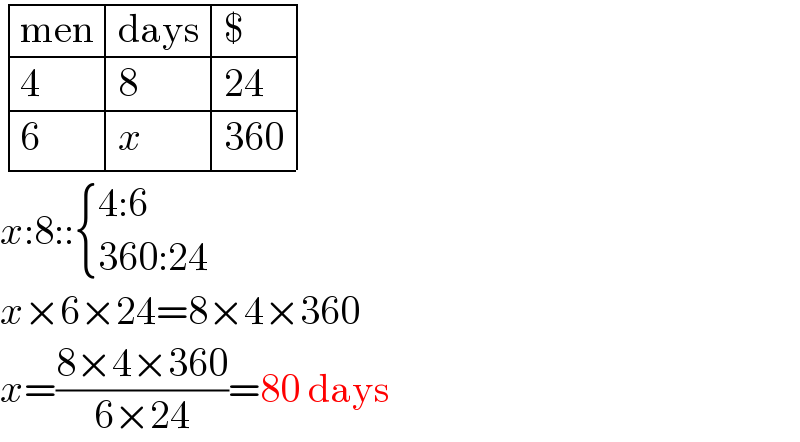
$$\begin{array}{|c|c|c|}{\mathrm{men}}&\hline{\mathrm{days}}&\hline{\$}\\{\mathrm{4}}&\hline{\mathrm{8}}&\hline{\mathrm{24}}\\{\mathrm{6}}&\hline{{x}}&\hline{\mathrm{360}}\\\hline\end{array} \\ $$$${x}:\mathrm{8}::\begin{cases}{\mathrm{4}:\mathrm{6}}\\{\mathrm{360}:\mathrm{24}}\end{cases} \\ $$$${x}×\mathrm{6}×\mathrm{24}=\mathrm{8}×\mathrm{4}×\mathrm{360} \\ $$$${x}=\frac{\mathrm{8}×\mathrm{4}×\mathrm{360}}{\mathrm{6}×\mathrm{24}}=\mathrm{80}\:\mathrm{days} \\ $$
Commented by Ar Brandon last updated on 02/Jan/22
Really?! OK Sir. Thanks
Commented by Ar Brandon last updated on 02/Jan/22
Is this some sort of cross-multiplication?
Commented by Rasheed.Sindhi last updated on 03/Jan/22

$$\mathcal{T}{he}\:{problem}\:{is}\:{somewhat}\:{strange}. \\ $$$${It}\:{is}\:{not}\:{dependant}\:{on}\:{amount}\:{of} \\ $$$${work}! \\ $$$$\begin{array}{|c|c|c|c|c|}{\mathrm{men}}&\hline{\mathrm{days}}&\hline{\$}\\{\underset{\mathrm{6}} {\mathrm{4}}\:\:\:\downarrow}&\hline{\underset{{x}} {\mathrm{8}}\:\:\uparrow}&\hline{\underset{\mathrm{360}} {\mathrm{24}}\:\:\uparrow}\\{\underset{\underset{\left({inverse}\:{proportion}\right)} {\rightarrow{days}\:\boldsymbol{{decrease}}}} {{men}\:\boldsymbol{{increase}}}}&\hline{}&\hline{\underset{\underset{\left({direct}\:{proportion}\right)} {\rightarrow{days}\:\boldsymbol{{increase}}}} {{dollars}\:\boldsymbol{{increase}}}}\\{\mathrm{4}:\mathrm{6}}&\hline{{x}:\mathrm{8}}&\hline{\mathrm{360}:\mathrm{24}}\\{\underset{\mathrm{A}} {\underbrace{{x}:\mathrm{8}::\mathrm{4}:\mathrm{6}}}}&\hline{}&\hline{\underset{{B}} {\underbrace{{x}:\mathrm{8}::\mathrm{360}:\mathrm{24}}}}\\\hline\end{array} \\ $$$$\mathrm{A}\cup\mathrm{B}: \\ $$$${x}:\mathrm{8}::\begin{cases}{\mathrm{4}:\mathrm{6}}\\{\mathrm{360}:\mathrm{24}}\end{cases} \\ $$$${x}×\mathrm{6}×\mathrm{24}=\mathrm{8}×\mathrm{4}×\mathrm{360} \\ $$$${x}=\frac{\mathrm{8}×\mathrm{4}×\mathrm{360}}{\mathrm{6}×\mathrm{24}}=\mathrm{80}\:\mathrm{days} \\ $$
Commented by Rasheed.Sindhi last updated on 03/Jan/22

$$\mathcal{T}{his}\:{is}\:{by}\:'{proportion}\:{method}'\:{while} \\ $$$${sir}\:{mr}\:{W}\:'{s}\:{method}\:\left({comment}\:{to}\:\right. \\ $$$$\left.{the}\:{question}\right)\:{is}\:'{unitary}\:{method}' \\ $$$$\mathcal{T}{his}\:{is}\:{a}\:{compound}\:{proportion}. \\ $$
Commented by Rasheed.Sindhi last updated on 03/Jan/22
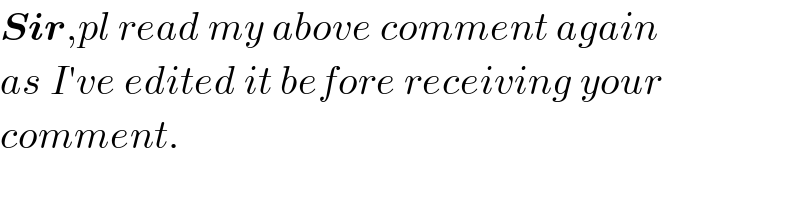
$$\boldsymbol{{Sir}},{pl}\:{read}\:{my}\:{above}\:{comment}\:{again} \\ $$$${as}\:{I}'{ve}\:{edited}\:{it}\:{before}\:{receiving}\:{your} \\ $$$${comment}. \\ $$
Commented by Rasheed.Sindhi last updated on 03/Jan/22

$$\left.{I}\:{have}\:{also}\:{sampathy}\:{for}\:{them}:\right) \\ $$$${But}\:\boldsymbol{{sir}},\:{the}\:{question}\:{says}: \\ $$$$\mathrm{4}\:{men}…..\mid\mathrm{6}{men}……{clear}\:\boldsymbol{{same}}\:\boldsymbol{{farm}}. \\ $$$${that}\:{is}\:{do}\:\boldsymbol{{same}}\:\boldsymbol{{quantity}}\:\boldsymbol{{of}}\:\boldsymbol{{work}}. \\ $$
Commented by mr W last updated on 03/Jan/22

$$“{clear}\:{the}\:{same}\:{farm}''\:{doesn}'{t}\:{define} \\ $$$${the}\:{quantity}\:{of}\:{the}\:{work},\:{only}\:{the} \\ $$$${type}\:{of}\:{the}\:{work},\:{i}\:{think}.\:\:{it}\:{could}\:{be} \\ $$$${that}\:{the}\:\mathrm{4}\:{men}\:{cleared}\:{the}\:{first}\:\mathrm{120}\:{m}^{\mathrm{2}} \\ $$$${of}\:{the}\:{farm}\:{in}\:\mathrm{8}\:{days}\:{for}\:{totally}\:\mathrm{24\$}, \\ $$$${and}\:{the}\:\mathrm{6}\:{men}\:{cleared}\:{the}\:{remaining} \\ $$$$\mathrm{1800}\:{m}^{\mathrm{2}} \:{of}\:{the}\:{same}\:{farm}\:{in}\:\mathrm{80}\:{days} \\ $$$${for}\:{totally}\:\mathrm{360\$}.\:{the}\:{same}\:{farm}\:{pays} \\ $$$${the}\:{same}\:{money}\:{for}\:{each}\:{man}\:{and} \\ $$$${each}\:{day}.\:{different}\:{farms}\:{may}\:{pay} \\ $$$${less}\:{or}\:{more}.\:{therefore}\:{it}\:{makes} \\ $$$${sinse}\:{to}\:{state}\:{that}\:{they}\:{cleared}\:{the} \\ $$$${same}\:{farm}.\:{this}\:{is}\:{my}\:{opinion}. \\ $$
Commented by mr W last updated on 03/Jan/22

$${but}\:{no}\:{matter}\:{how}\:{it}\:{is},\:\mathrm{4}\:{men}\:{earn} \\ $$$${only}\:\mathrm{24\$}\:{in}\:\mathrm{8}\:{days},\:{that}'{s}\:{definitely} \\ $$$$\left.{too}\:{less},\:{i}\:{think}\::\right) \\ $$
Commented by Rasheed.Sindhi last updated on 03/Jan/22

$$\mathrm{Okay}\:\mathrm{sir},\:{you}'{re}\:{keen}\:{obserer},{no}\:{doubt}! \\ $$$$“\mathrm{4}\:\mathrm{men}\:\mathrm{clear}\:\mathrm{a}\:\mathrm{farm}…''{means}\:{they} \\ $$$${clear}\:\boldsymbol{{whole}}\:{farm}.“…\mathrm{6}\:\mathrm{men}\:\mathrm{take} \\ $$$$\mathrm{to}\:\mathrm{clear}\:\mathrm{the}\:\mathrm{same}\:\mathrm{farm}'',{doesn}'{t}\:\:{again}\:{it}\: \\ $$$${mean}\:{the}\:{whole}\:{farm}? \\ $$
Commented by mr W last updated on 03/Jan/22

$${actually}\:{i}\:{thought}\:{the}\:{same}\:{as}\:{you}. \\ $$$${but}\:{then}\:{i}\:{got}\:{a}\:{problem}\:{with}\:{the}\:{logic}. \\ $$$${so}\:{i}\:{just}\:{changed}\:{my}\:{opinion}\:{in}\:{order} \\ $$$${to}\:{become}\:{conform}\:{with}\:{the}\:{solution}. \\ $$
Commented by mr W last updated on 03/Jan/22

$${this}\:{is}\:{the}\:{logic}\:{problem}\:{i}\:{mentioned}. \\ $$$$“{clear}\:{a}\:{farm}''\:{and}\:“{clear}\:{the}\:{same} \\ $$$${farm}''\:{may}\:{not}\:{mean}\:{the}\:{same}\:{work} \\ $$$${done},\:{because}\:{one}\:{can}\:{not}\:{pay}\:{for}\:{the} \\ $$$${same}\:{work}\:{done}\:{in}\:{one}\:{time}\:{only}\:\mathrm{24\$}\: \\ $$$${and}\:{in}\:{an}\:{other}\:{time}\:\mathrm{360\$}.\:{certainly}\: \\ $$$${in}\:{reality}\:{it}'{s}\:{possible},\:{but}\:{in}\: \\ $$$${mathematics}\:{it}'{s}\:{not}\:{possible}. \\ $$$${because}\:{there}\:{is}\:{no}\:{mathematics}\:{if} \\ $$$${there}\:{is}\:{no}\:{ligic}.\:{therefore}\:“{clear}\:{a}\: \\ $$$${farm}''\:{and}\:“{clear}\:{the}\:{same}\:{farm}'' \\ $$$${can}\:{logically}\:{only}\:{mean}\:{the}\:{type}\:{of} \\ $$$${the}\:{work},\:{i}.{e}.\:“{clear}\:{in}\:{a}\:{farm}''\:{as}\: \\ $$$${well}\:{as}\:“{clear}\:{in}\:{the}\:{same}\:{farm}''. \\ $$$${i}\:{think}\:{the}\:{guy}\:{who}\:{originally}\:{wrote}\: \\ $$$${this}\:{question}\:{is}\:{no}\:{lawyer},\:{even}\:{no} \\ $$$${native}\:{speaker}\:{of}\:{english},\:\:{like}\:{you} \\ $$$${and}\:{me}.\:{therefore}\:{we}\:{should}\:{look}\:{more} \\ $$$${at}\:{the}\:{logic}\:{behind}\:{it}\:{instead}\:{of}\:{the} \\ $$$${wording}. \\ $$
Commented by Rasheed.Sindhi last updated on 03/Jan/22

$$\mathbb{T}_{\mathbb{H}_{\mathbb{AN}} \mathbb{K}} \mathbb{S}\:\mathbb{S}_{\mathbb{I}_{\mathbb{R}!} } \\ $$👍👍👍👍👍
