Menu Close

4x-1-2x-2-3x-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 123793 by liberty last updated on 28/Nov/20
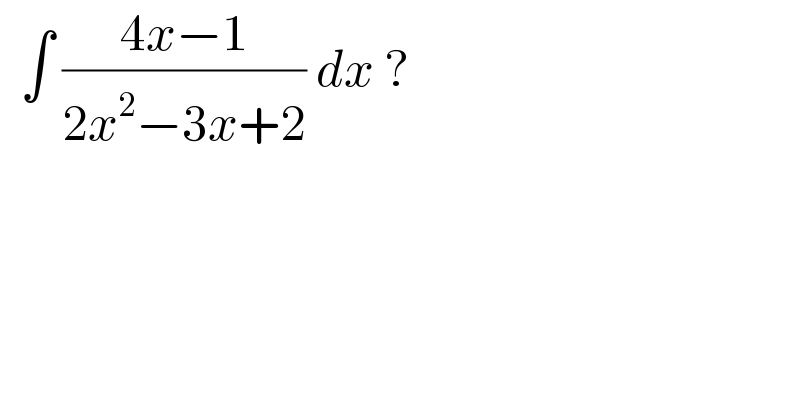
∫ ((4x−1)/(2x^2 −3x+2)) dx ?
$$\:\:\int\:\frac{\mathrm{4}{x}−\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}}\:{dx}\:? \\ $$
Answered by Dwaipayan Shikari last updated on 28/Nov/20
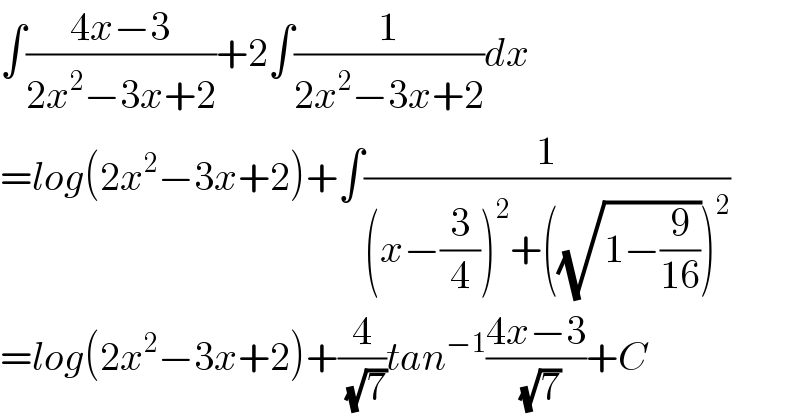
∫((4x−3)/(2x^2 −3x+2))+2∫(1/(2x^2 −3x+2))dx =log(2x^2 −3x+2)+∫(1/((x−(3/4))^2 +((√(1−(9/(16)))))^2 )) =log(2x^2 −3x+2)+(4/( (√7)))tan^(−1) ((4x−3)/( (√7)))+C
$$\int\frac{\mathrm{4}{x}−\mathrm{3}}{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}}+\mathrm{2}\int\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}}{dx} \\ $$$$={log}\left(\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}\right)+\int\frac{\mathrm{1}}{\left({x}−\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{1}−\frac{\mathrm{9}}{\mathrm{16}}}\right)^{\mathrm{2}} } \\ $$$$={log}\left(\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}\right)+\frac{\mathrm{4}}{\:\sqrt{\mathrm{7}}}{tan}^{−\mathrm{1}} \frac{\mathrm{4}{x}−\mathrm{3}}{\:\sqrt{\mathrm{7}}}+{C} \\ $$
Answered by liberty last updated on 28/Nov/20
partial fraction ((4x−1)/(2x^2 −3x+2)) = P (((d/dx)(2x^2 −3x+2))/(2x^2 −3x+2))+(Q/(2x^2 −3x+2)) 4x−1 = P(4x−3)+Q ; { ((P=1)),((−1=Q−3P ;Q=2)) :} I(x)=∫((4x−3)/(2x^2 −3x+2)) dx + ∫ (2/(2(x^2 −((3x)/2)+1)))dx I(x)= ℓn ∣2x^2 −3x+2∣ + ∫ (dx/((x−(3/4))^2 +(((√7)/4))^2 )) I(x)= ℓn ∣2x^2 −3x+2∣+(4/( (√7))) arctan (((x−(3/4))/((√7)/4))) +c I(x)=ln ∣2x^2 −3x+2∣ +(4/( (√7)))arctan (((4x−3)/( (√7))))+c
$$\:{partial}\:{fraction}\:\frac{\mathrm{4}{x}−\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}}\:=\:{P}\:\frac{\frac{{d}}{{dx}}\left(\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}\right)}{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}}+\frac{{Q}}{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}} \\ $$$$\mathrm{4}{x}−\mathrm{1}\:=\:{P}\left(\mathrm{4}{x}−\mathrm{3}\right)+{Q}\:;\:\begin{cases}{{P}=\mathrm{1}}\\{−\mathrm{1}={Q}−\mathrm{3}{P}\:;{Q}=\mathrm{2}}\end{cases} \\ $$$${I}\left({x}\right)=\int\frac{\mathrm{4}{x}−\mathrm{3}}{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}}\:{dx}\:+\:\int\:\frac{\mathrm{2}}{\mathrm{2}\left({x}^{\mathrm{2}} −\frac{\mathrm{3}{x}}{\mathrm{2}}+\mathrm{1}\right)}{dx} \\ $$$${I}\left({x}\right)=\:\ell{n}\:\mid\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}\mid\:+\:\int\:\frac{{dx}}{\left({x}−\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{7}}}{\mathrm{4}}\right)^{\mathrm{2}} } \\ $$$${I}\left({x}\right)=\:\ell{n}\:\mid\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}\mid+\frac{\mathrm{4}}{\:\sqrt{\mathrm{7}}}\:\mathrm{arctan}\:\left(\frac{{x}−\frac{\mathrm{3}}{\mathrm{4}}}{\frac{\sqrt{\mathrm{7}}}{\mathrm{4}}}\right)\:+\mathrm{c} \\ $$$$\mathrm{I}\left({x}\right)=\mathrm{ln}\:\mid\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}\mid\:+\frac{\mathrm{4}}{\:\sqrt{\mathrm{7}}}\mathrm{arctan}\:\left(\frac{\mathrm{4}{x}−\mathrm{3}}{\:\sqrt{\mathrm{7}}}\right)+{c}\: \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *