Menu Close

4x-1-8x-3-x-2-x-4-2x-2-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 120102 by benjo_mathlover last updated on 29/Oct/20
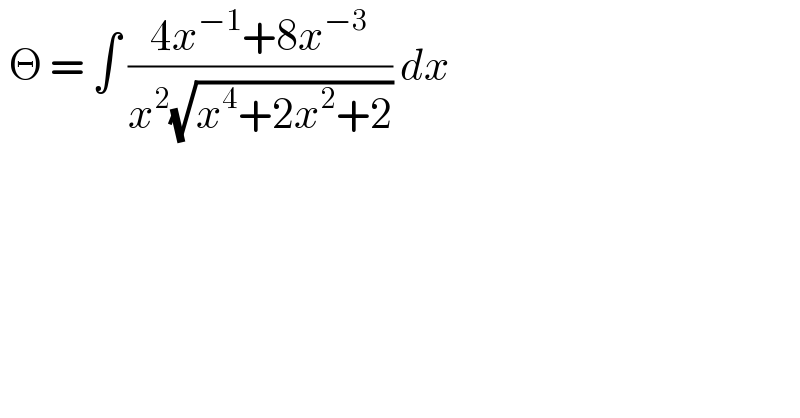
Θ = ∫ ((4x^(−1) +8x^(−3) )/(x^2 (√(x^4 +2x^2 +2)))) dx
$$\:\Theta\:=\:\int\:\frac{\mathrm{4}{x}^{−\mathrm{1}} +\mathrm{8}{x}^{−\mathrm{3}} }{{x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}}}\:{dx}\: \\ $$
Answered by mathmax by abdo last updated on 29/Oct/20
I =∫ ((4x^(−1) +8x^(−3) )/(x^2 (√(x^4 +2x^2 +2))))dx ⇒I=∫ ((4x^2 +8)/(x^5 (√(x^4 +2x^2 +2))))dx ⇒ I=_(x^2 =t) ∫ ((4t+8)/(t^(5/2) (√(t^2 +2t+2))))(dt/(2(√t))) =∫ ((2t+4)/(t^3 (√(t^2 +2t+2))))dt =∫ ((2t+4)/(t^3 (√((t+1)^2 +1))))dt =_(t+1=sh(t)) ∫ ((2(sht−1)+4)/((sht−1)^3 ch(t)))ch(t)dt =∫ ((2sht+2)/(sh^3 t−3sh^2 t +3sht −1))dt =∫ ((2((e^t −e^(−t) )/2)+2)/((((e^t −e^(−t) )/2))^3 −3(((e^t −e^(−t) )/(2 )))^2 +3((e^t −e^(−t) )/2)−1))dt =_(e^t =u) ∫ ((u−u^(−1) +2)/((1/8)(u−u^(−1) )^3 −(3/4)(u−u^(−1) )^2 +(3/2)(u−u^(−1) )−1))(du/u) =8 ∫ ((u−u^(−1) +2)/(u{ (u−u^(−1) )^3 −6(u−u^(−1) )^2 +12(u−u^(−1) )−8}))du =8∫ ((u−u^(−1) +2)/(u{ u^3 −3u^2 u^(−1) +3uu^(−2) +u^(−3) −6(u^2 −2+u^(−1) )+12u−12u^(−1) −8}))du =8 ∫ ((u−u^(−1) +2)/(u{u^3 −3u+3u^(−1) +u^(−3) −6u^2 +12−6u^(−1) +12u−12u^(−1) −8})) =8∫ ((u−u^(−1) +2)/(u{u^3 −3u+3u^(−1) +u^(−3) −6u^2 +12u−18u^(−1) −8}))du =8∫ ((u−u^(−1) +2)/(u^4 −3u^2 +3+u^(−2) −6u^3 +12u^2 −18+8u))du =8∫ ((u^3 −u+2u^2 )/(u^6 +9u^4 +3u^2 +1−6u^5 −18u^2 +8u^3 ))du =8∫ ((u^3 +2u^2 −u)/(u^6 −6u^5 +9u^4 +8u^3 −15u^2 +1))du rest decompositon of F(u) =((u^3 +2u^2 −u)/(u^6 −6u^5 +9u^4 +8u^3 −15u^2 +1))....be continued....
$$\mathrm{I}\:=\int\:\:\frac{\mathrm{4x}^{−\mathrm{1}} +\mathrm{8x}^{−\mathrm{3}} }{\mathrm{x}^{\mathrm{2}} \sqrt{\mathrm{x}^{\mathrm{4}} +\mathrm{2x}^{\mathrm{2}} +\mathrm{2}}}\mathrm{dx}\:\Rightarrow\mathrm{I}=\int\:\:\frac{\mathrm{4x}^{\mathrm{2}} +\mathrm{8}}{\mathrm{x}^{\mathrm{5}} \sqrt{\mathrm{x}^{\mathrm{4}} +\mathrm{2x}^{\mathrm{2}} +\mathrm{2}}}\mathrm{dx}\:\Rightarrow \\ $$$$\mathrm{I}=_{\mathrm{x}^{\mathrm{2}} =\mathrm{t}} \:\:\:\:\int\:\:\:\frac{\mathrm{4t}+\mathrm{8}}{\mathrm{t}^{\frac{\mathrm{5}}{\mathrm{2}}} \sqrt{\mathrm{t}^{\mathrm{2}} +\mathrm{2t}+\mathrm{2}}}\frac{\mathrm{dt}}{\mathrm{2}\sqrt{\mathrm{t}}}\:=\int\:\:\frac{\mathrm{2t}+\mathrm{4}}{\mathrm{t}^{\mathrm{3}} \sqrt{\mathrm{t}^{\mathrm{2}} +\mathrm{2t}+\mathrm{2}}}\mathrm{dt} \\ $$$$=\int\:\:\frac{\mathrm{2t}+\mathrm{4}}{\mathrm{t}^{\mathrm{3}} \sqrt{\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}}}\mathrm{dt}\:=_{\mathrm{t}+\mathrm{1}=\mathrm{sh}\left(\mathrm{t}\right)} \:\:\int\:\:\frac{\mathrm{2}\left(\mathrm{sht}−\mathrm{1}\right)+\mathrm{4}}{\left(\mathrm{sht}−\mathrm{1}\right)^{\mathrm{3}} \mathrm{ch}\left(\mathrm{t}\right)}\mathrm{ch}\left(\mathrm{t}\right)\mathrm{dt} \\ $$$$=\int\:\:\frac{\mathrm{2sht}+\mathrm{2}}{\mathrm{sh}^{\mathrm{3}} \mathrm{t}−\mathrm{3sh}^{\mathrm{2}} \mathrm{t}\:+\mathrm{3sht}\:−\mathrm{1}}\mathrm{dt} \\ $$$$=\int\:\:\:\frac{\mathrm{2}\frac{\mathrm{e}^{\mathrm{t}} −\mathrm{e}^{−\mathrm{t}} }{\mathrm{2}}+\mathrm{2}}{\left(\frac{\mathrm{e}^{\mathrm{t}} −\mathrm{e}^{−\mathrm{t}} }{\mathrm{2}}\right)^{\mathrm{3}} −\mathrm{3}\left(\frac{\mathrm{e}^{\mathrm{t}} −\mathrm{e}^{−\mathrm{t}} }{\mathrm{2}\:\:}\right)^{\mathrm{2}} +\mathrm{3}\frac{\mathrm{e}^{\mathrm{t}} −\mathrm{e}^{−\mathrm{t}} }{\mathrm{2}}−\mathrm{1}}\mathrm{dt} \\ $$$$=_{\mathrm{e}^{\mathrm{t}} \:=\mathrm{u}} \:\:\:\:\int\:\:\:\frac{\mathrm{u}−\mathrm{u}^{−\mathrm{1}} +\mathrm{2}}{\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{u}−\mathrm{u}^{−\mathrm{1}} \right)^{\mathrm{3}} −\frac{\mathrm{3}}{\mathrm{4}}\left(\mathrm{u}−\mathrm{u}^{−\mathrm{1}} \right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{2}}\left(\mathrm{u}−\mathrm{u}^{−\mathrm{1}} \right)−\mathrm{1}}\frac{\mathrm{du}}{\mathrm{u}} \\ $$$$=\mathrm{8}\:\int\:\frac{\mathrm{u}−\mathrm{u}^{−\mathrm{1}} +\mathrm{2}}{\mathrm{u}\left\{\:\:\left(\mathrm{u}−\mathrm{u}^{−\mathrm{1}} \right)^{\mathrm{3}} −\mathrm{6}\left(\mathrm{u}−\mathrm{u}^{−\mathrm{1}} \right)^{\mathrm{2}} +\mathrm{12}\left(\mathrm{u}−\mathrm{u}^{−\mathrm{1}} \right)−\mathrm{8}\right\}}\mathrm{du} \\ $$$$=\mathrm{8}\int\:\:\:\frac{\mathrm{u}−\mathrm{u}^{−\mathrm{1}} +\mathrm{2}}{\mathrm{u}\left\{\:\mathrm{u}^{\mathrm{3}} −\mathrm{3u}^{\mathrm{2}} \mathrm{u}^{−\mathrm{1}} +\mathrm{3uu}^{−\mathrm{2}} +\mathrm{u}^{−\mathrm{3}} −\mathrm{6}\left(\mathrm{u}^{\mathrm{2}} −\mathrm{2}+\mathrm{u}^{−\mathrm{1}} \right)+\mathrm{12u}−\mathrm{12u}^{−\mathrm{1}} −\mathrm{8}\right\}}\mathrm{du} \\ $$$$=\mathrm{8}\:\int\:\:\:\:\frac{\mathrm{u}−\mathrm{u}^{−\mathrm{1}} +\mathrm{2}}{\mathrm{u}\left\{\mathrm{u}^{\mathrm{3}} −\mathrm{3u}+\mathrm{3u}^{−\mathrm{1}} +\mathrm{u}^{−\mathrm{3}} −\mathrm{6u}^{\mathrm{2}} +\mathrm{12}−\mathrm{6u}^{−\mathrm{1}} +\mathrm{12u}−\mathrm{12u}^{−\mathrm{1}} −\mathrm{8}\right\}} \\ $$$$=\mathrm{8}\int\:\:\frac{\mathrm{u}−\mathrm{u}^{−\mathrm{1}} +\mathrm{2}}{\mathrm{u}\left\{\mathrm{u}^{\mathrm{3}} −\mathrm{3u}+\mathrm{3u}^{−\mathrm{1}} \:+\mathrm{u}^{−\mathrm{3}} −\mathrm{6u}^{\mathrm{2}} +\mathrm{12u}−\mathrm{18u}^{−\mathrm{1}} −\mathrm{8}\right\}}\mathrm{du} \\ $$$$=\mathrm{8}\int\:\:\frac{\mathrm{u}−\mathrm{u}^{−\mathrm{1}} +\mathrm{2}}{\mathrm{u}^{\mathrm{4}} −\mathrm{3u}^{\mathrm{2}} +\mathrm{3}+\mathrm{u}^{−\mathrm{2}} −\mathrm{6u}^{\mathrm{3}} +\mathrm{12u}^{\mathrm{2}} \:−\mathrm{18}+\mathrm{8u}}\mathrm{du} \\ $$$$=\mathrm{8}\int\:\:\:\frac{\mathrm{u}^{\mathrm{3}} −\mathrm{u}+\mathrm{2u}^{\mathrm{2}} }{\mathrm{u}^{\mathrm{6}} +\mathrm{9u}^{\mathrm{4}} \:+\mathrm{3u}^{\mathrm{2}} \:+\mathrm{1}−\mathrm{6u}^{\mathrm{5}} −\mathrm{18u}^{\mathrm{2}} \:+\mathrm{8u}^{\mathrm{3}} }\mathrm{du} \\ $$$$=\mathrm{8}\int\:\:\frac{\mathrm{u}^{\mathrm{3}} +\mathrm{2u}^{\mathrm{2}} −\mathrm{u}}{\mathrm{u}^{\mathrm{6}} −\mathrm{6u}^{\mathrm{5}} +\mathrm{9u}^{\mathrm{4}} +\mathrm{8u}^{\mathrm{3}} −\mathrm{15u}^{\mathrm{2}} +\mathrm{1}}\mathrm{du}\:\:\mathrm{rest}\:\mathrm{decompositon}\:\mathrm{of} \\ $$$$\mathrm{F}\left(\mathrm{u}\right)\:=\frac{\mathrm{u}^{\mathrm{3}} +\mathrm{2u}^{\mathrm{2}} −\mathrm{u}}{\mathrm{u}^{\mathrm{6}} −\mathrm{6u}^{\mathrm{5}} \:+\mathrm{9u}^{\mathrm{4}} \:+\mathrm{8u}^{\mathrm{3}} −\mathrm{15u}^{\mathrm{2}} \:+\mathrm{1}}….\mathrm{be}\:\mathrm{continued}…. \\ $$$$ \\ $$$$ \\ $$
Answered by TANMAY PANACEA last updated on 29/Oct/20
∫((4x^(−1) +8x^(−3) )/(x^2 (√(1+(x^2 +1)^2 ))))dx 4∫((x^2 +2)/(x^5 (√(1+(x^2 +1)^2 ))))dx x^2 +1=tana→2xdx=sec^2 ada dx=((sec^2 ada)/(2(√(−1+tana)))) 4∫((1+tana)/((−1+tana)^(5/2) ×seca))×((sec^2 ada)/(2(√(−1+tana)))) 2∫((1+tana)/((−1+tana)^3 ))×secada 2∫(((sina+cosa))/(cosa(sina−cosa)^3 ))×cos^3 a×(da/(cosa)) 2∫cosa×((sina+cosa)/((sina−cosa)^3 ))da (I/2)=cosa∫((sina+cosa)/((sina−cosa)^3 ))−∫[(d/da)(cosa)∫((sina+cosa)/((sina−cosa)^3 ))]da ■■ look d(sina−cosa)=cosa+sina so ∫((sina+cosa)/((sina−cosa)^3 ))da=∫((d(sina−cosa))/((sina−cosa)^3 )) =(1/(−2(sina−cosa)^2 )) ■■ (I/2)=cosa×(1/(−2(sina−cosa)^2 ))−∫((−sina)/1)×(1/(−2(sina−cosa)^2 ))da I=cosa×(1/(−(sina−cosa)^2 ))−∫((sina)/((sina−cosa)^2 )) I=((cosa)/(−(sina−cos)^2 ))−I_★ I_★ =(1/2)∫((sina+cosa+sina−cosa)/((sina−cosa)^2 ))da (1/2)∫((d(sina−cosa))/((sina−cosa)^2 ))+(1/2)∫(da/(sina−cosa)) (1/2)×((−1)/((sina−cosa)))+(1/2)∫(((√2) da)/(sin(a−(π/4)))) ((−1)/(2(sina−cosa)))+(1/( (√2)))lntan((a/2)−(π/8))+c note tana=1+x^2 pls chk pls <
$$\int\frac{\mathrm{4}{x}^{−\mathrm{1}} +\mathrm{8}{x}^{−\mathrm{3}} }{{x}^{\mathrm{2}} \sqrt{\mathrm{1}+\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }}{dx} \\ $$$$\mathrm{4}\int\frac{{x}^{\mathrm{2}} +\mathrm{2}}{{x}^{\mathrm{5}} \sqrt{\mathrm{1}+\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }}{dx} \\ $$$${x}^{\mathrm{2}} +\mathrm{1}={tana}\rightarrow\mathrm{2}{xdx}={sec}^{\mathrm{2}} {ada} \\ $$$${dx}=\frac{{sec}^{\mathrm{2}} {ada}}{\mathrm{2}\sqrt{−\mathrm{1}+{tana}}} \\ $$$$\mathrm{4}\int\frac{\mathrm{1}+{tana}}{\left(−\mathrm{1}+{tana}\right)^{\frac{\mathrm{5}}{\mathrm{2}}} ×{seca}}×\frac{{sec}^{\mathrm{2}} {ada}}{\mathrm{2}\sqrt{−\mathrm{1}+{tana}}} \\ $$$$\mathrm{2}\int\frac{\mathrm{1}+{tana}}{\left(−\mathrm{1}+{tana}\right)^{\mathrm{3}} }×{secada} \\ $$$$\mathrm{2}\int\frac{\left({sina}+{cosa}\right)}{{cosa}\left({sina}−{cosa}\right)^{\mathrm{3}} }×{cos}^{\mathrm{3}} {a}×\frac{{da}}{{cosa}} \\ $$$$\mathrm{2}\int{cosa}×\frac{{sina}+{cosa}}{\left({sina}−{cosa}\right)^{\mathrm{3}} }{da} \\ $$$$\frac{{I}}{\mathrm{2}}={cosa}\int\frac{{sina}+{cosa}}{\left({sina}−{cosa}\right)^{\mathrm{3}} }−\int\left[\frac{{d}}{{da}}\left({cosa}\right)\int\frac{{sina}+{cosa}}{\left({sina}−{cosa}\right)^{\mathrm{3}} }\right]{da} \\ $$$$\blacksquare\blacksquare\:{look} \\ $$$${d}\left({sina}−{cosa}\right)={cosa}+{sina} \\ $$$${so}\:\int\frac{{sina}+{cosa}}{\left({sina}−{cosa}\right)^{\mathrm{3}} }{da}=\int\frac{{d}\left({sina}−{cosa}\right)}{\left({sina}−{cosa}\right)^{\mathrm{3}} } \\ $$$$=\frac{\mathrm{1}}{−\mathrm{2}\left({sina}−{cosa}\right)^{\mathrm{2}} }\:\blacksquare\blacksquare \\ $$$$\frac{{I}}{\mathrm{2}}={cosa}×\frac{\mathrm{1}}{−\mathrm{2}\left({sina}−{cosa}\right)^{\mathrm{2}} }−\int\frac{−{sina}}{\mathrm{1}}×\frac{\mathrm{1}}{−\mathrm{2}\left({sina}−{cosa}\right)^{\mathrm{2}} }{da} \\ $$$${I}={cosa}×\frac{\mathrm{1}}{−\left({sina}−{cosa}\right)^{\mathrm{2}} }−\int\frac{{sina}}{\left({sina}−{cosa}\right)^{\mathrm{2}} } \\ $$$$\boldsymbol{{I}}=\frac{{cosa}}{−\left({sina}−{cos}\right)^{\mathrm{2}} }−{I}_{\bigstar} \\ $$$${I}_{\bigstar} =\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{sina}+{cosa}+{sina}−{cosa}}{\left({sina}−{cosa}\right)^{\mathrm{2}} }{da} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({sina}−{cosa}\right)}{\left({sina}−{cosa}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{da}}{{sina}−{cosa}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\frac{−\mathrm{1}}{\left({sina}−{cosa}\right)}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\sqrt{\mathrm{2}}\:{da}}{{sin}\left({a}−\frac{\pi}{\mathrm{4}}\right)} \\ $$$$\frac{−\mathrm{1}}{\mathrm{2}\left({sina}−{cosa}\right)}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{lntan}\left(\frac{{a}}{\mathrm{2}}−\frac{\pi}{\mathrm{8}}\right)+{c} \\ $$$$\boldsymbol{{note}}\:\boldsymbol{{tana}}=\mathrm{1}+\boldsymbol{{x}}^{\mathrm{2}} \\ $$$${pls}\:{chk}\:{pls} \\ $$$$< \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *