Question Number 64130 by ANTARES VY last updated on 14/Jul/19
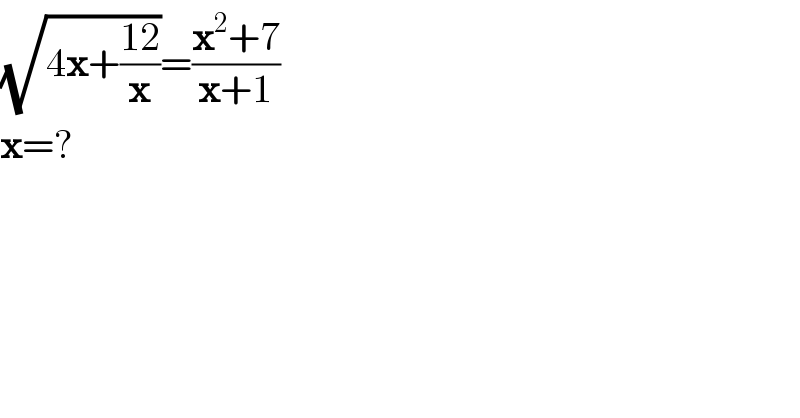
$$\sqrt{\mathrm{4}\boldsymbol{\mathrm{x}}+\frac{\mathrm{12}}{\boldsymbol{\mathrm{x}}}}=\frac{\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{7}}{\boldsymbol{\mathrm{x}}+\mathrm{1}} \\ $$$$\boldsymbol{\mathrm{x}}=? \\ $$
Commented by Prithwish sen last updated on 14/Jul/19

$$\mathrm{x}=\:\mathrm{1},\mathrm{1},\mathrm{3}\:\mathrm{and}\:\frac{−\mathrm{1}\pm\mathrm{15i}}{\mathrm{2}} \\ $$
Answered by mr W last updated on 14/Jul/19
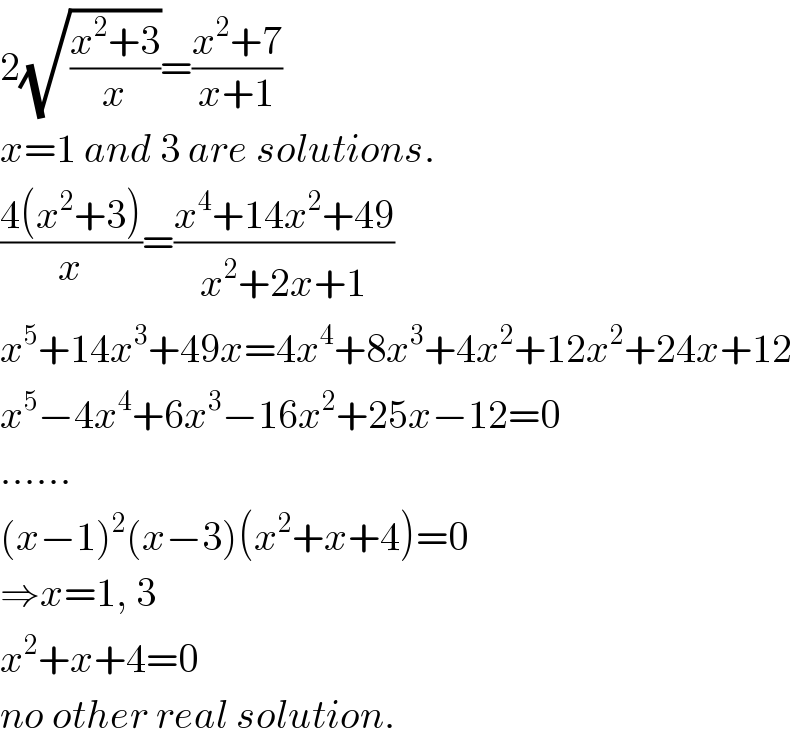
$$\mathrm{2}\sqrt{\frac{{x}^{\mathrm{2}} +\mathrm{3}}{{x}}}=\frac{{x}^{\mathrm{2}} +\mathrm{7}}{{x}+\mathrm{1}} \\ $$$${x}=\mathrm{1}\:{and}\:\mathrm{3}\:{are}\:{solutions}. \\ $$$$\frac{\mathrm{4}\left({x}^{\mathrm{2}} +\mathrm{3}\right)}{{x}}=\frac{{x}^{\mathrm{4}} +\mathrm{14}{x}^{\mathrm{2}} +\mathrm{49}}{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}} \\ $$$${x}^{\mathrm{5}} +\mathrm{14}{x}^{\mathrm{3}} +\mathrm{49}{x}=\mathrm{4}{x}^{\mathrm{4}} +\mathrm{8}{x}^{\mathrm{3}} +\mathrm{4}{x}^{\mathrm{2}} +\mathrm{12}{x}^{\mathrm{2}} +\mathrm{24}{x}+\mathrm{12} \\ $$$${x}^{\mathrm{5}} −\mathrm{4}{x}^{\mathrm{4}} +\mathrm{6}{x}^{\mathrm{3}} −\mathrm{16}{x}^{\mathrm{2}} +\mathrm{25}{x}−\mathrm{12}=\mathrm{0} \\ $$$$…… \\ $$$$\left({x}−\mathrm{1}\right)^{\mathrm{2}} \left({x}−\mathrm{3}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{4}\right)=\mathrm{0} \\ $$$$\Rightarrow{x}=\mathrm{1},\:\mathrm{3} \\ $$$${x}^{\mathrm{2}} +{x}+\mathrm{4}=\mathrm{0}\: \\ $$$${no}\:{other}\:{real}\:{solution}. \\ $$
Answered by ajfour last updated on 14/Jul/19

$$\mathrm{4}\left({x}^{\mathrm{2}} +\mathrm{3}\right)\left({x}+\mathrm{1}\right)^{\mathrm{2}} ={x}\left({x}^{\mathrm{2}} +\mathrm{7}\right)^{\mathrm{2}} \\ $$$${let}\:\:\:\:\mathrm{4}{a}^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{3}\right)={x} \\ $$$$\:\:\&\:\:\:{x}+\mathrm{1}={a}\left({x}^{\mathrm{2}} +\mathrm{7}\right) \\ $$$$\Rightarrow\:\:{x}=\frac{\mathrm{1}}{\mathrm{8}{a}^{\mathrm{2}} }\pm\sqrt{\frac{\mathrm{1}}{\mathrm{64}{a}^{\mathrm{4}} }−\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:{x}=\frac{\mathrm{1}}{\mathrm{2}{a}}\pm\sqrt{\frac{\mathrm{1}}{\mathrm{4}{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{a}}−\mathrm{7}} \\ $$$${let}\:{the}\:{irrational}\:\&\:{rational}\:{parts}\:{be}\:{equal} \\ $$$$\Rightarrow\:\:{a}=\frac{\mathrm{1}}{\mathrm{4}}\:\:\&\:\:{we}\:{see}\:{that}\:{for}\:{this} \\ $$$${value}\:{the}\:{irrational}\:{parts}\:{are} \\ $$$${both}\:{same}\:\left(=\mathrm{1}\right). \\ $$$${hence}\:\:\:\:\:{x}=\:\mathrm{2}\pm\mathrm{1}\:\:. \\ $$$$\Rightarrow\:\:{real}\:{roots}\:{are}\:\:{x}=\mathrm{1},\mathrm{3}\:. \\ $$
