Question Number 85153 by reprins last updated on 19/Mar/20
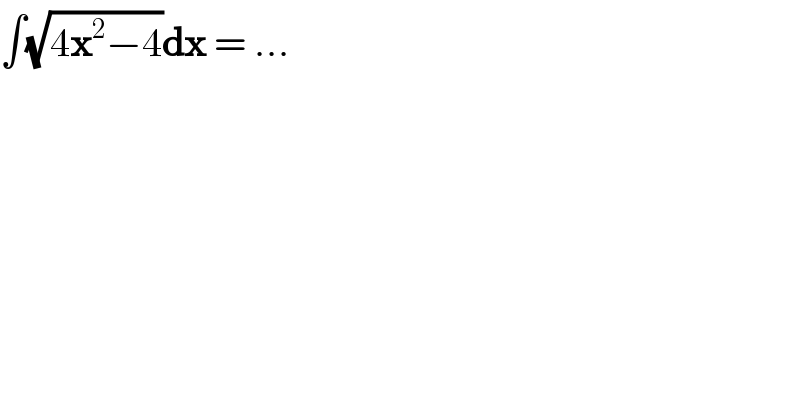
$$\int\sqrt{\mathrm{4}\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{4}}\boldsymbol{\mathrm{dx}}\:=\:… \\ $$$$ \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 19/Mar/20
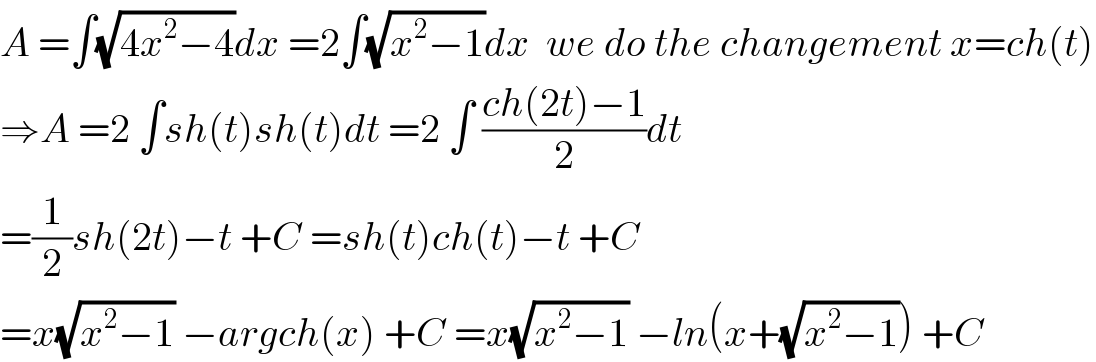
$${A}\:=\int\sqrt{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}}{dx}\:=\mathrm{2}\int\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}{dx}\:\:{we}\:{do}\:{the}\:{changement}\:{x}={ch}\left({t}\right) \\ $$$$\Rightarrow{A}\:=\mathrm{2}\:\int{sh}\left({t}\right){sh}\left({t}\right){dt}\:=\mathrm{2}\:\int\:\frac{{ch}\left(\mathrm{2}{t}\right)−\mathrm{1}}{\mathrm{2}}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{sh}\left(\mathrm{2}{t}\right)−{t}\:+{C}\:={sh}\left({t}\right){ch}\left({t}\right)−{t}\:+{C} \\ $$$$={x}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\:−{argch}\left({x}\right)\:+{C}\:={x}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\:−{ln}\left({x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\right)\:+{C} \\ $$
Answered by john santu last updated on 19/Mar/20
![2∫(√(x^2 −1)) dx =K let x = sec t K= 2∫ (√(sec^2 t−1)) sec t tan t dt K= 2 ∫ sec t tan^2 t dt K = 2[∫ sec^3 t dt − ln ∣sec t + tan t ∣ ] for I= ∫ sec^3 t dt = ∫ sec t d(tan t) I = sec t tan t − ∫ tan^2 t sec t dt I = sec t tan t − ∫ sec^3 t dt + ln ∣sec t+tan t∣ 2I = sec t tan t + ln ∣sec t+tan t∣ I = (1/2)sec t tan t +(1/2) ln ∣sec t+tan t∣ K = sec t tan t − ln ∣sec t+tan t∣ + c ∴ K = x(√(x^2 −1 )) −ln ∣x+(√(x^2 −1)) ∣ +c](https://www.tinkutara.com/question/Q85221.png)
$$\mathrm{2}\int\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\:\mathrm{dx}\:=\mathrm{K} \\ $$$$\mathrm{let}\:\mathrm{x}\:=\:\mathrm{sec}\:\mathrm{t}\: \\ $$$$\mathrm{K}=\:\mathrm{2}\int\:\sqrt{\mathrm{sec}\:^{\mathrm{2}} \mathrm{t}−\mathrm{1}}\:\mathrm{sec}\:\mathrm{t}\:\mathrm{tan}\:\mathrm{t}\:\mathrm{dt} \\ $$$$\mathrm{K}=\:\mathrm{2}\:\int\:\mathrm{sec}\:\mathrm{t}\:\mathrm{tan}\:^{\mathrm{2}} \mathrm{t}\:\mathrm{dt}\: \\ $$$$\mathrm{K}\:=\:\mathrm{2}\left[\int\:\mathrm{sec}\:^{\mathrm{3}} \mathrm{t}\:\mathrm{dt}\:−\:\mathrm{ln}\:\mid\mathrm{sec}\:\mathrm{t}\:+\:\mathrm{tan}\:\mathrm{t}\:\mid\:\right] \\ $$$$\mathrm{for}\:\mathrm{I}=\:\int\:\mathrm{sec}\:^{\mathrm{3}} \mathrm{t}\:\mathrm{dt}\:=\:\int\:\mathrm{sec}\:\mathrm{t}\:\mathrm{d}\left(\mathrm{tan}\:\mathrm{t}\right) \\ $$$$\mathrm{I}\:=\:\mathrm{sec}\:\mathrm{t}\:\mathrm{tan}\:\mathrm{t}\:−\:\int\:\mathrm{tan}\:^{\mathrm{2}} \mathrm{t}\:\mathrm{sec}\:\mathrm{t}\:\mathrm{dt} \\ $$$$\mathrm{I}\:=\:\mathrm{sec}\:\mathrm{t}\:\mathrm{tan}\:\mathrm{t}\:−\:\int\:\mathrm{sec}\:^{\mathrm{3}} \mathrm{t}\:\mathrm{dt}\:+\:\mathrm{ln}\:\mid\mathrm{sec}\:\mathrm{t}+\mathrm{tan}\:\mathrm{t}\mid \\ $$$$\mathrm{2I}\:=\:\mathrm{sec}\:\mathrm{t}\:\mathrm{tan}\:\mathrm{t}\:+\:\mathrm{ln}\:\mid\mathrm{sec}\:\mathrm{t}+\mathrm{tan}\:\mathrm{t}\mid \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sec}\:\mathrm{t}\:\mathrm{tan}\:\mathrm{t}\:+\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{ln}\:\mid\mathrm{sec}\:\mathrm{t}+\mathrm{tan}\:\mathrm{t}\mid \\ $$$$\mathrm{K}\:=\:\mathrm{sec}\:\mathrm{t}\:\mathrm{tan}\:\mathrm{t}\:−\:\mathrm{ln}\:\mid\mathrm{sec}\:\mathrm{t}+\mathrm{tan}\:\mathrm{t}\mid\:+\:\mathrm{c} \\ $$$$\therefore\:\mathrm{K}\:=\:\mathrm{x}\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}\:}\:−\mathrm{ln}\:\mid\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\:\mid\:+\mathrm{c} \\ $$
